8.1 Stream Erosion and Deposition
As we discussed in Lab 5, flowing water is a very important mechanism for erosion, transportation and deposition of sediments. Water flow in a stream is primarily related to the stream’s gradient, but it is also controlled by the geometry of the stream channel. As shown in Figure 8.1.1, water flow velocity is decreased by friction along the stream bed, so it is slowest at the bottom and edges and fastest near the surface and in the middle. In fact, the velocity just below the surface is typically a little higher than right at the surface because of friction between the water and the air. On a curved section of a stream, flow is fastest on the outside and slowest on the inside.
![Figure 8.1.1: The relative velocity of stream flow depending on whether the stream channel is straight or curved (left), and with respect to the water depth (right). [Image Description]](https://pressbooks.openeducationalberta.ca/app/uploads/sites/66/2019/06/meandering-1024x376.png)
Other factors that affect stream-water velocity are the size of sediments on the stream bed—because large particles tend to slow the flow more than small ones—and the discharge, or volume of water passing a point in a unit of time (e.g., cubic metres (m3) per second). During a flood, the water level always rises, so there is more cross-sectional area for the water to flow in, however, as long as a river remains confined to its channel, the velocity of the water flow also increases.
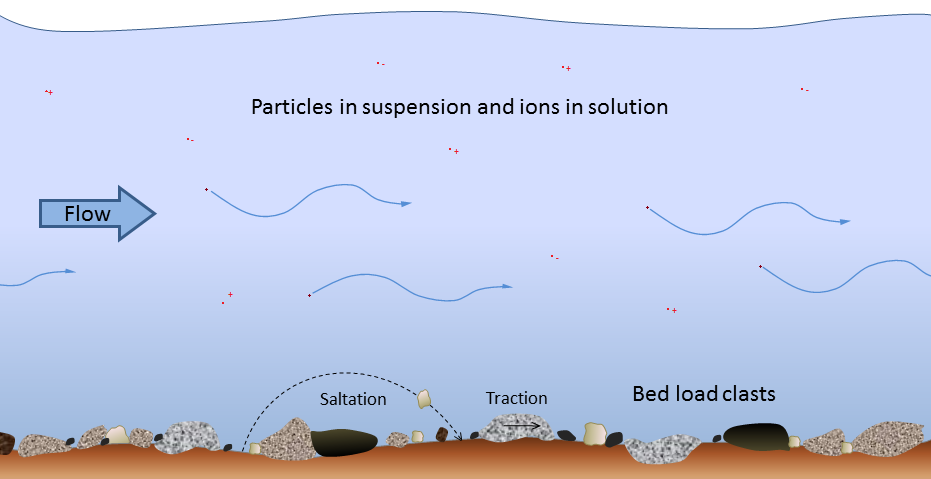
Figure 8.1.2 shows the nature of sediment transportation in a stream. Large particles rest on the bottom—bed load—and may only be moved during rapid flows under flood conditions. They can be moved by saltation (bouncing) and by traction (being pushed along by the force of the flow).
Smaller particles may rest on the bottom some of the time, where they can be moved by saltation and traction, but they can also be held in suspension in the flowing water, especially at higher velocities. As you know from intuition and from experience, streams that flow fast tend to be turbulent (flow paths are chaotic and the water surface appears rough) and the water may be muddy, while those that flow more slowly tend to have laminar flow (straight-line flow and a smooth water surface) and clear water. Turbulent flow is more effective than laminar flow at keeping sediments in suspension.
Stream water also has a dissolved load, which represents (on average) about 15% of the mass of material transported, and includes ions such as calcium (Ca+2) and chloride (Cl−) in solution. The solubility of these ions is not affected by flow velocity.
The faster the water is flowing, the larger the particles that can be kept in suspension and transported within the flowing water. However, as Swedish geographer Filip Hjulström discovered in the 1940s, the relationship between grain size and the likelihood of a grain being eroded, transported, or deposited is not as simple as one might imagine (Figure 8.1.3). Consider, for example, a 1 millimetre grain of sand. If it is resting on the bottom, it will remain there until the velocity is high enough to erode it, around 20 centimetres per second (cm/s). But once it is in suspension, that same 1 mm particle will remain in suspension as long as the velocity doesn’t drop below 10 cm/s. For a 10 mm gravel grain, the velocity is 105 cm/s to be eroded from the bed but only 80 cm/s to remain in suspension.
![Figure 8.1.3: The Hjulström-Sundborg diagram showing the relationships between particle size and the tendency to be eroded, transported, or deposited at different current velocities. [Image Description]](https://pressbooks.openeducationalberta.ca/app/uploads/sites/66/2020/06/hulstrom-2-300x203.png)
On the other hand, a 0.01 mm silt particle only needs a velocity of 0.1 centimetres per second (cm/s) to remain in suspension, but requires 60 cm/s to be eroded. In other words, a tiny silt grain requires a greater velocity to be eroded than a grain of sand that is 100 times larger! For clay-sized particles, the discrepancy is even greater. In a stream, the most easily eroded particles are small sand grains between 0.2 mm and 0.5 mm. Anything smaller or larger requires a higher water velocity to be eroded and entrained in the flow. The main reason for this is that small particles, and especially the tiny grains of clay, have a strong tendency to stick together, and so are difficult to erode from the stream bed.
It is important to be aware that a stream can both erode and deposit sediments at the same time. At 100 cm/s, for example, silt, sand, and medium gravel will be eroded from the stream bed and transported in suspension, coarse gravel will be held in suspension, pebbles will be both transported and deposited, and cobbles and boulders will remain stationary on the stream bed.
Practice Exercise 8.1: Understanding the Hjulström-Sundborg diagram
Refer to the Hjulström-Sundborg diagram (Figure 8.1.3) to answer these questions.
- A fine sand grain (0.1 millimetres) is resting on the bottom of a stream bed.
- What stream velocity will it take to get that sand grain into suspension?
- Once the particle is in suspension, the velocity starts to drop. At what velocity will it finally come back to rest on the stream bed?
- A stream is flowing at 10 centimetres per second (which means it takes 10 seconds to go 1 metres, and that’s pretty slow).
- What size of particles can be eroded at 10 centimetres per second?
- What is the largest particle that, once already in suspension, will remain in suspension at 10 centimetres per second?
See Appendix 2 for Practice Exercise 8.1 answers.
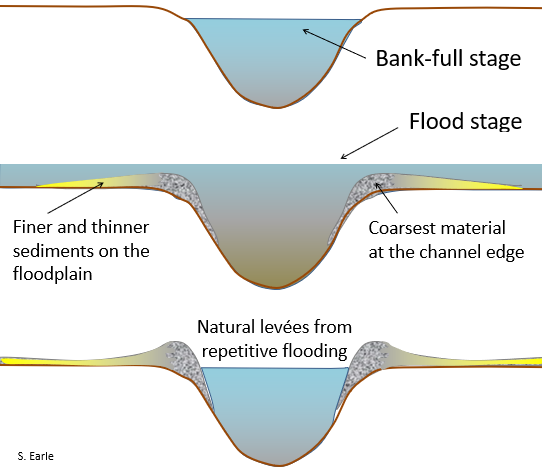
A stream typically reaches its greatest velocity when it is close to flooding over its banks. This is known as the bank-full stage, as shown in Figure 8.1.4. As soon as the flooding stream overtops its banks and occupies the wide area of its flood plain, the water has a much larger area to flow through and the velocity drops significantly. At this point, sediment that was being carried by the high-velocity water is deposited near the edge of the channel, forming a natural bank or levée.
Image Descriptions
Figure 8.1.1 image description: When a stream curves, the flow of water is fastest on the outside of the curve and slowest on the inside of the curve. When the stream is straight and a uniform depth, the stream flows fastest in the middle near the top and slowest along the edges. When the depth is not uniform, the stream flows fastest in the deeper section. [Return to Figure 8.1.1]
Figure 8.1.3 image description:
- Erosion velocity curve: A 0.001 millimetre particle would erode at a flow velocity of 500 centimetres per second or greater. As the particle size gets larger, the minimum flow velocity needed to erode the particle decreases, with the lowest flow velocity being 30 centimetres per second to erode a 0.5 millimetre particle. To erode particles larger than 0.5 millimetres, the minimum flow velocity rises again.
- Settling velocity curve: A 0.01 millimetre particle would be deposited with a flow velocity of 0.1 centimetre per second or less. As the flow velocity increases, only larger and larger particles will be deposited.
- Particles between these two curves (either moving too slow or being too small to be eroded or deposited) will be transported in the stream.
Media Attributions
- Figure 8.1.1, 8.1.2, 8.1.3, 8.1.4: © Steven Earle. CC BY.
the slope of a stream bed over a specific distance, typically expressed in m per km
The physical boundaries of a stream (or a river), consisting of a bed and stream (or river) banks.
the volume of water flow in a stream expressed in terms of volume per unit time (e.g., m3/s)
the fraction of a stream’s sediment load that typically rests on the bottom and is moved by saltation and traction
The vast majority of the minerals that make up the rocks of Earth's crust are silicate minerals. These include minerals such as quartz, feldspar, mica, amphibole, pyroxene, olivine, and a variety of clay minerals. The building block of all of these minerals is the silica tetrahedron, a combination of four oxygen atoms and one silicon atom. As we've seen, it's called a tetrahedron because planes drawn through the oxygen atoms form a shape with 4 surfaces (Figure 2.2.4). Since the silicon ion has a charge of 4 and each of the four oxygen ions has a charge of −2, the silica tetrahedron has a net charge of −4.
In silicate minerals, these tetrahedra are arranged and linked together in a variety of ways, from single units to complex frameworks (Table 2.6). The simplest silicate structure, that of the mineral olivine, is composed of isolated tetrahedra bonded to iron and/or magnesium ions. In olivine, the −4 charge of each silica tetrahedron is balanced by two divalent (i.e., +2) iron or magnesium cations. Olivine can be either Mg2SiO4 or Fe2SiO4, or some combination of the two (Mg,Fe)2SiO4. The divalent cations of magnesium and iron are quite close in radius (0.73 versus 0.62 angstroms[1]). Because of this size similarity, and because they are both divalent cations (both can have a charge of +2), iron and magnesium can readily substitute for each other in olivine and in many other minerals.
| [Skip Table] | ||
| Tetrahedron Configuration Picture | Tetrahedron Configuration Name | Example Minerals |
|---|---|---|
 |
Isolated (nesosilicates) | Olivine, garnet, zircon, kyanite |
 |
Pairs (sorosilicates) | Epidote, zoisite |
 |
Rings (cyclosilicates) | Tourmaline |
 |
Single chains (inosilicates) | Pyroxenes, wollastonite |
 |
Double chains (inosilicates) | Amphiboles |
 |
Sheets (phyllosilicates) | Micas, clay minerals, serpentine, chlorite |
| 3-dimensional structure | Framework (tectosilicates) | Feldspars, quartz, zeolite |

Cut around the outside of the shape (solid lines and dotted lines), and then fold along the solid lines to form a tetrahedron. If you have glue or tape, secure the tabs to the tetrahedron to hold it together. If you don’t have glue or tape, make a slice along the thin grey line and insert the pointed tab into the slit.
If you are doing this in a classroom, try joining your tetrahedron with others into pairs, rings, single and double chains, sheets, and even three-dimensional frameworks.
See Appendix 3 for Exercise 2.3 answers.
In olivine, unlike most other silicate minerals, the silica tetrahedra are not bonded to each other. Instead they are bonded to the iron and/or magnesium ions, in the configuration shown on Figure 2.4.1.

As already noted, the 2 ions of iron and magnesium are similar in size (although not quite the same). This allows them to substitute for each other in some silicate minerals. In fact, the ions that are common in silicate minerals have a wide range of sizes, as depicted in Figure 2.4.2. All of the ions shown are cations, except for oxygen. Note that iron can exist as both a +2 ion (if it loses two electrons during ionization) or a +3 ion (if it loses three). Fe2+ is known as ferrous iron. Fe3+ is known as ferric iron. Ionic radii are critical to the composition of silicate minerals, so we’ll be referring to this diagram again.

The structure of the single-chain silicate pyroxene is shown on Figures 2.4.3 and 2.4.4. In pyroxene, silica tetrahedra are linked together in a single chain, where one oxygen ion from each tetrahedron is shared with the adjacent tetrahedron, hence there are fewer oxygens in the structure. The result is that the oxygen-to-silicon ratio is lower than in olivine (3:1 instead of 4:1), and the net charge per silicon atom is less (−2 instead of −4). Therefore, fewer cations are necessary to balance that charge. Pyroxene compositions are of the type MgSiO3, FeSiO3, and CaSiO3, or some combination of these. Pyroxene can also be written as (Mg,Fe,Ca)SiO3, where the elements in the brackets can be present in any proportion. In other words, pyroxene has one cation for each silica tetrahedron (e.g., MgSiO3) while olivine has two (e.g., Mg2SiO4). Because each silicon ion is +4 and each oxygen ion is −2, the three oxygens (−6) and the one silicon (+4) give a net charge of −2 for the single chain of silica tetrahedra. In pyroxene, the one divalent cation (2) per tetrahedron balances that −2 charge. In olivine, it takes two divalent cations to balance the −4 charge of an isolated tetrahedron.The structure of pyroxene is more “permissive” than that of olivine—meaning that cations with a wider range of ionic radii can fit into it. That’s why pyroxenes can have iron (radius 0.63 Å) or magnesium (radius 0.72 Å) or calcium (radius 1.00 Å) cations (see Figure 2.4.2 above).


Exercise 2.4 Oxygen deprivation
The diagram below represents a single chain in a silicate mineral. Count the number of tetrahedra versus the number of oxygen ions (yellow spheres). Each tetrahedron has one silicon ion so this should give you the ratio of Si to O in single-chain silicates (e.g., pyroxene).
The diagram below represents a double chain in a silicate mineral. Again, count the number of tetrahedra versus the number of oxygen ions. This should give you the ratio of Si to O in double-chain silicates (e.g., amphibole).
See Appendix 3 for Exercise 2.4 answers.
In amphibole structures, the silica tetrahedra are linked in a double chain that has an oxygen-to-silicon ratio lower than that of pyroxene, and hence still fewer cations are necessary to balance the charge. Amphibole is even more permissive than pyroxene and its compositions can be very complex. Hornblende, for example, can include sodium, potassium, calcium, magnesium, iron, aluminum, silicon, oxygen, fluorine, and the hydroxyl ion (OH−).
In mica structures, the silica tetrahedra are arranged in continuous sheets, where each tetrahedron shares three oxygen anions with adjacent tetrahedra. There is even more sharing of oxygens between adjacent tetrahedra and hence fewer cations are needed to balance the charge of the silica-tetrahedra structure in sheet silicate minerals. Bonding between sheets is relatively weak, and this accounts for the well-developed one-directional cleavage in micas (Figure 2.4.5). Biotite mica can have iron and/or magnesium in it and that makes it a ferromagnesian silicate mineral (like olivine, pyroxene, and amphibole). Chlorite is another similar mineral that commonly includes magnesium. In muscovite mica, the only cations present are aluminum and potassium; hence it is a non-ferromagnesian silicate mineral.

Apart from muscovite, biotite, and chlorite, there are many other sheet silicates (a.k.a. phyllosilicates), many of which exist as clay-sized fragments (i.e., less than 0.004 millimetres). These include the clay minerals kaolinite, illite, and smectite, and although they are difficult to study because of their very small size, they are extremely important components of rocks and especially of soils.
All of the sheet silicate minerals also have water molecules within their structure.
Silica tetrahedra are bonded in three-dimensional frameworks in both the feldspars and quartz. These are non-ferromagnesian minerals—they don't contain any iron or magnesium. In addition to silica tetrahedra, feldspars include the cations aluminum, potassium, sodium, and calcium in various combinations. Quartz contains only silica tetrahedra.
The three main feldspar minerals are potassium feldspar, (a.k.a. K-feldspar or K-spar) and two types of plagioclase feldspar: albite (sodium only) and anorthite (calcium only). As is the case for iron and magnesium in olivine, there is a continuous range of compositions (solid solution series) between albite and anorthite in plagioclase. Because the calcium and sodium ions are almost identical in size (1.00 Å versus 0.99 Å) any intermediate compositions between CaAl2Si3O8 and NaAlSi3O8 can exist (Figure 2.4.6). This is a little bit surprising because, although they are very similar in size, calcium and sodium ions don’t have the same charge (Ca2+ versus Na+ ). This problem is accounted for by the corresponding substitution of Al+3 for Si+4 . Therefore, albite is NaAlSi3O8 (1 Al and 3 Si) while anorthite is CaAl2Si2O8 (2 Al and 2 Si), and plagioclase feldspars of intermediate composition have intermediate proportions of Al and Si. This is called a “coupled-substitution.”
The intermediate-composition plagioclase feldspars are oligoclase (10% to 30% Ca), andesine (30% to 50% Ca), labradorite (50% to 70% Ca), and bytownite (70% to 90% Ca). K-feldspar (KAlSi3O8) has a slightly different structure than that of plagioclase, owing to the larger size of the potassium ion (1.37 Å) and because of this large size, potassium and sodium do not readily substitute for each other, except at high temperatures. These high-temperature feldspars are likely to be found only in volcanic rocks because intrusive igneous rocks cool slowly enough to low temperatures for the feldspars to change into one of the lower-temperature forms.

In quartz (SiO2), the silica tetrahedra are bonded in a “perfect” three-dimensional framework. Each tetrahedron is bonded to four other tetrahedra (with an oxygen shared at every corner of each tetrahedron), and as a result, the ratio of silicon to oxygen is 1:2. Since the one silicon cation has a +4 charge and the two oxygen anions each have a −2 charge, the charge is balanced. There is no need for aluminum or any of the other cations such as sodium or potassium. The hardness and lack of cleavage in quartz result from the strong covalent/ionic bonds characteristic of the silica tetrahedron.
Exercise 2.5 Ferromagnesian silicates?
Silicate minerals are classified as being either ferromagnesian or non-ferromagnesian depending on whether or not they have iron (Fe) and/or magnesium (Mg) in their formula. A number of minerals and their formulas are listed below. For each one, indicate whether or not it is a ferromagnesian silicate.
| Mineral | Formula | Ferromagnesian silicate? |
| olivine | (Mg,Fe)2SiO4 | . |
| pyrite | FeS2 | . |
| plagioclase feldspar | CaAl2Si2O8 | . |
| pyroxene | MgSiO3 | . |
| hematite | Fe2O3 | . |
| orthoclase feldspar | KAlSi3O8 | . |
| quartz | SiO2 | . |
| amphibole | Fe7Si8O22(OH)2 | . |
| muscovite | K2Al4Si6Al2O20(OH)4 | . |
| magnetite | Fe3O4 | . |
| biotite | K2Fe4Al2Si6Al4O20(OH)4 | . |
| dolomite | (Ca,Mg)CO3 | . |
| garnet | Fe2Al2Si3O12 | . |
| serpentine | Mg3Si2O5(OH)4 | . |
See Appendix 3 for Exercise 2.5 answers.*Some of the formulas, especially the more complicated ones, have been simplified.
Image Descriptions
along a stream, the ridge that naturally forms along the edge of the channel during flood events



