Very large and very small: numbers and units in Earth science
Learning Outcomes
By the end of this section you should be able to
- Make simple calculations and conversions using scientific format for very large and very small numbers
- Express the precision of a measurement using an appropriate number of significant figures
- Use SI and other units correctly
Exponential or scientific format

Large numbers
Earth science involves numbers that are very small and very large. It’s important to ask “how small” or “how large” when observations are expressed in these terms. For very small and large numbers we typically use exponential format.
The number of seconds in a year is 31,556,926. We can write this in exponential format as:
3.1556926 x 107 s
or, on many calculators
3.1556926 E+7
In this number, the “x 107″ (“times ten to the power seven”) means that to get from 3.1556926 to the real number of seconds in a year you need to shift the decimal point 7 places to the right.
In this format, the value 3.1556936 is known as the coefficient (or sometimes mantissa), and the “7” is known as the exponent.
Usually, you won’t see all seven digits of the coefficient written out. If we are not concerned about extreme accuracy, we can approximate to three significant figures:
3.16×107 s
If you expand this approximate value, by shifting the decimal point 7 places right, it comes out to 31,600,000.0; notice that, because there are now only three digits in the coefficient, you have to add zeros to get the decimal point in the right place.
Small numbers
Exponential format can be used for very small numbers too. For number smaller than one, the exponent is negative. For example the radius of an oxygen atom is about 0.00000000006 m or:
6×10-11 m
What this means is that to get from “6” to the true value, it’s necessary to shift the decimal point 11 places left. Once again, the gap is filled in by zeros.
0.00000000006
Multiplying and dividing
There are some useful rules for arithmetic when using numbers in exponential format. For example, suppose we want to multiply two large numbers together. To take a simple example, multiply 20,000 by 3,500. Done longhand, this comes out to 70,000,000. In exponential format, it’s
2×104 × 3.5×103 = 7×107
Notice that we multiply together the coefficients, but we just have to add the exponents.
Conversely, if we divide one number in exponential format by another we have to subtract the exponents.
7×107 ÷ 2×104 = 2×103
Precision and approximation
It’s also important to ask how precise a numerical observation is. If we say that two plates are moving past each other at 10 cm/yr, is that exactly 10 or could it be 9.9 or 10.3? In some cases the precision can be indicated by using an appropriate number of significant figures: ~10 (approximately 10) or just 10, or 10.0, or 10.00. For more detailed work it’s common to express precision with a plus or minus figure, for example
10.0 ± 0.3 cm/yr
Exponential format provides a convenient way of expressing precision. The number of digits in the coefficient, called the number of significant figures indicates roughly how precisely a quantity is known.
For example, the number of seconds in a year is known very precisely, so we can use eight significant figures:
3.1556926 x 107 s
On the other hand, if the radius of the sun is only known to about five significant figures, we would write:
1.3927 × 106 km
Logarithms
It’s easy to understand how numbers like 10, 100, 1000 can be expressed as 101, 102, 103, but it turns out that any number can be expressed in the form 10x. For example, the number 3 is equal to 100.47712. In this expression, the number 0.47712 is known as the logarithm or log to base ten of the number 3.
log10(3) = 0.47712.
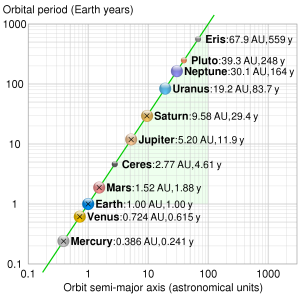
In the days before calculators, addition and subraction of numbers was much easier to do than multiplication and division, so numbers were routinely converted to logarithms to help with complex calculation. Although logarithms are no longer used this way, when dealing with very variable quantities it’s often convenient to plot graphs on which the axes are logarithms. In the following example, a logarithmic scale is used, so that each step along the graph axis represents a multiplication by ten. This makes for a convenient plot that also displays an interesting mathematical relationship (known as Kepler’s second law) between the two quantities.
Sometimes logs are expressed relative to number bases other than 10. One particularly useful type of logarithm is expressed relative to base e where e = 2.7182818284. Logs expressed in this way are known as natural logarithms, sometimes abbreviated ln. Natural logarithms are used in the calculation of rates of radioactive decay. Most scientific calculators will calculate logs to base ten and natural logarithms.
Units
Scientific measurements are almost always expressed in the metric system, and usually in a standardized version of the metric system called Système Internationale or SI. In the SI system larger and smaller units are given names based on a standard system of prefixes.
For example, the SI unit of distance is the metre[1], abbreviated m. Longer distances can be expressed in kilometres, abbreviated km, where one kilometre (1 km) is 103 m. Shorter distances can be expressed in millimetres (mm) where one millimetre (1 mm) is 10-3m.
Larger values are expressed using the following prefixes:
| Prefix | Abbreviation | Multiplies the size by… |
| kilo- | k | 103 |
| mega- | M | 106 |
| giga- | B | 109 |
| tera- | T | 1012 |
| peta- | P | 1015 |
Notice that each unit is a thousand times larger than the previous one.
For very small units we use the following.
| Prefix | Abbreviation | Multiplies the size by… |
| milli- | m | 10-3 |
| micro- | μ | 10-6 |
| nano- | n | 10-9 |
In the above table each unit is one thousand times smaller than the previous one.
The SI system defines many other units, for all kinds of physical quantities. Some of the most important are:
| Phenomenon | Unit | Abbreviation |
| Mass | kilogram | kg |
| Time | second | s |
| Temperature (above absolute zero) | kelvin | K |
| Energy | joule | J |
| Force | newton | N |
| Power (rate of energy flow) | watt | W |
| Pressure or stress (force per unit area) | pascal | Pa |
Phenomena for which there are no named units are given derived unit names. For example, speeds of objects are measured in metres per second, abbreviated to m/s or alternatively ms-1.
There are some important tips for writing SI units.
- Be careful of capitalization. For example kg means kilogram or kilograms but Kg means Kelvin-grams.
- The same abbreviation is used regardless of whether the number is singular or plural. Never try to make SI units plural by adding an s. If you write kms to mean kilometres it may be read as kilometre-seconds!
- Always put a space between digits and the abbreviation, unless the abbreviation is the degrees symbol °.
Some units used in Earth science are derived units, that are not the primary S.I. unit for measuring a phenomenon but are nonetheless used by scientists in various fields. Some examples that you may encounter elsewhere in the text are as follows:
| Derived unit | Meaning | Abbreviation |
| astronomical unit | Distance from Earth to Sun 1.49597870700×1011 m | A.U. |
| tonne | 1 Megagram or 1,000 kg | t |
| acceleration due to gravity | 9.81 ms-2 | g |
| degrees Celsius | Degrees above freezing point of water | °C |
| bar | 105 pascals | bar |
| year | 31,556,926 seconds | yr |
| kilo-annum | Thousands of years ago | ka |
| mega-annum | Millions of years ago | Ma |
| giga-annum | Billions of years ago | Ga |
| Proportion: percent | parts per hundred | % |
| Proportion: tenths of a percent | parts per thousand | ‰ |
| Proportion: parts per million | parts per million | ppm |
Sometimes, particularly in the USA, scientific measurements are converted into imperial or non-metric units (e.g., miles, degrees Farenheit, pounds per square inch) for popular consumption in the news media. Most scientists do not use such units in their work, and we avoid them in this book.
- Most of the world uses the spellings metre, kilometre, millimetre, as used here. In the USA, the units are spelled meter, kilometer, millimeter. ↵
A way of representing large or small numbers using a coefficient or mantissa (typically a number with one digit to the left of the decimal point) multiplied by an exponent (a power of 10)

