Chapter 5: Skeletal Muscle Contraction
Brian R MacIntosh

Learning Objectives
After studying this Chapter, you should be able to:
-
- Explain the sliding filament theory of muscle contraction
- Explain how the cross-bridge theory works
- Describe the process of excitation-contraction coupling
- Compare action potentials of muscle and nerve
- Explain the aspects of muscle contraction that dictate energy cost
- Describe the location and function of various calcium handling proteins in muscle
- Draw a diagram illustrating the activation of muscle including calcium handling
- Describe the relationship between frequency of activation and summation of force
- Describe the relationship between frequency of activation and calcium concentration
- Draw graphs and explain the fundamental properties of skeletal muscle, including:
- force-pCa2+-relationship
- moment-angle relationship
- moment-angular velocity relationship
- force-length relationship
- force-frequency relationship
- length dependence of force development
- force-velocity relationship
- force-power relationship and power-velocity relationship
Key Terms
filament, active force, Ca2+ sensitivity, calcium transient, cross-bridge theory, receptor, dynamometer, electromyography, endocytosis, exocytosis, fixed end contraction, force-frequency relationship, force-length relationship, force-pCa2+ relationship, force-velocity relationship, in vitro, in vivo, isometric contraction, length dependent activation, motor unit, muscle contraction, myosin filament, myosin head, optimal length, passive force, pCa2+, stroke, power-velocity relationship, ryanodine receptor, sarcoplasmic reticulum, SERCA, sliding filament theory, summation, terminal cisternae, tetanic contraction, transverse tubule, tropomyosin, troponin, twitch contraction, ultrasound imaging, weak and strong-binding
—
Case Study: Isokinetic Muscle Function Test
Julia has been recruited to be a subject in a research study at the University of Winnipeg. Part of the study requires that she be tested on a Biodex to determine her moment-angular velocity relationship. This is analogous to the force-velocity relationship but expresses the relationship between joint and angular velocity rather than the linear force-velocity relationship. Julia has been given strict instructions on her activity and diet leading into the test session. She is not to engage in any vigorous physical activity for 24 hours prior to the testing and she is to eat only a light breakfast at least 2 hours before her testing session at 11:00 AM.
Procedures During Julia’s Biodex Test
On her arrival at the laboratory, Julia has electromyographic electrodes placed on the skin of her right leg. Application of these electrodes requires careful skin preparation (the area is shaved, then lightly abraded with sandpaper, cleaned with an alcohol swab, then the self-adhesive electrodes are applied once the skin has dried). EMG electrodes are typically applied in pairs with alignment in the direction of the underlying muscle fibres. The muscle fibre direction can be confirmed with ultrasound, though in most cases investigators will know the approximate alignment of fibres. Julia has electrodes placed on her biceps femoris, rectus femoris, vastus lateralis, and vastus medialis. A ground or common electrode is placed on her patella. She is allowed to warm-up for 15 min on a cycle ergometer, then she rests for 10 minutes. Julia is then strapped to the Biodex chair (hips, chest, and thigh straps) and range of motion is assessed by passive movement of the knee from full flexion to full extension. The chair limits knee flexion beyond 90 degrees and full extension means the knee comes to 180 degrees. Julia is given an emergency switch to use if the machine moves her leg to an uncomfortable position.
Julia is instructed to practice with submaximal effort at a variety of angular velocities. It feels strange to do these muscle contractions because the speed of movement is restricted by the Biodex. When Julia pushes harder, she notices that the machine does not move faster. When the machine is set to higher speeds, Julia has difficulty maintaining effort because the lever arm moves so quickly. This is her second time using this machine and it still feels strange.
Data collection for this study requires Julia to perform maximal effort isometric (fixed-end) contractions at each of several joint angles, in random order. These contractions allow formulation of the relationship between and joint angle, analogous to the force-length relationship. Each contraction lasts 4-5 seconds with 4 min between sequential contractions to minimize fatigue. Following this, she is given 10 minute rest before maximal effort contractions are obtained at each of 8 angular velocities, again in random order. These contractions allow determination of the moment-angular velocity relationship. By the time Julia has finished the series of contractions, her leg muscles feel worn out.
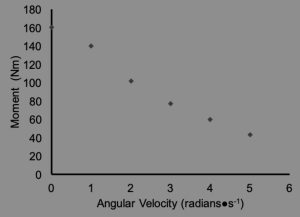
In Figure 5-1, Julia’s results for the second series of contractions are presented. Here, the torque generated at the knee during extension at a variety of angular velocities is presented. The relationship is nearly linear, but a slight curve can be detected. Note that the maximal velocity in this figure is 5 rad·s-1. Clearly, the knee joint can be extended at a faster angular velocity, but measurement of the moment during these movements is challenging. Tihanyi and colleagues (1982) overcame this obstacle by creating their own equipment to measure the relationship between moment and angular velocity at high relative angular velocities and found that the maximal rate of knee extension should be 14-18 rad·s-1. The subjects for this study were high and long jumpers.
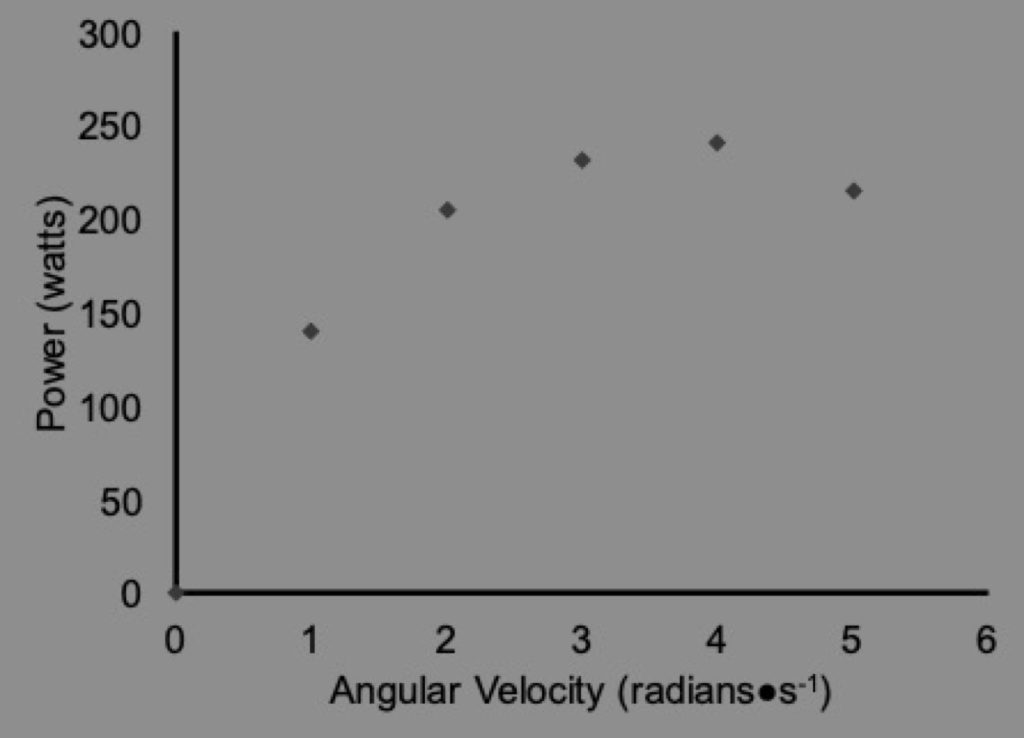
Figure 5-2 presents the power-angular velocity relationship for Julia’s tests. Here, it can be seen that power is low when angular velocity is low and rises to a peak around 4 rad·s-1. When the angular velocity is higher than this, power decreases. It is known that power is zero when angular velocity is zero and when torque is zero.
Overview
Now, it is time to see how our muscles function. Muscle has a pretty simple function; it either contracts or it relaxes. Muscle contraction is the process of turning on and generating force which, if the load is not too great, allows motion. Alternatively, if the load can overcome the force generated by the muscle, lengthening will occur. Without muscle contraction, we are immobile lumps of tissue. Muscle can be stretched passively to permit range of motion, contract without length change to hold position or maintain posture and can shorten or elongate while contracting to achieve motion or slow the rate of movement.
Imagine that you do not know much about the structure of muscle. This is necessary to grasp that in the early 50’s we did not have a good understanding of how muscle worked. In this chapter, before the mechanism of contraction in skeletal muscle is described, the early understanding of muscle is presented. Following this, a couple of long-standing yet perhaps incomplete theories are presented. Following this, the energy requiring processes are described. It is important to understand that although muscle contraction is a simple biochemical reaction between proteins , this reaction cannot occur without the use of chemical energy, in the form of adenosine triphosphate (ATP). ATP is the universal form of chemical energy used through-out the body.
Regulating the contraction of muscle is important. We can voluntarily turn muscle on and choose to stop activation and allow muscle to relax. This process of turning muscle on and off requires the interaction of the nervous system and in particular the motor pathways of the central nervous system and the motor neurons of the peripheral nervous system. Action potentials on the motor axons travel to individual muscle fibres, activating them to contract. At the neuromuscular junction, nerve terminal activation is transferred to muscle activation and a sequence of events referred to as excitation-contraction coupling is initiated. This sequence results in turning on muscle contraction. There is no “off” switch for muscle. Relaxation is initiated by stopping activation.
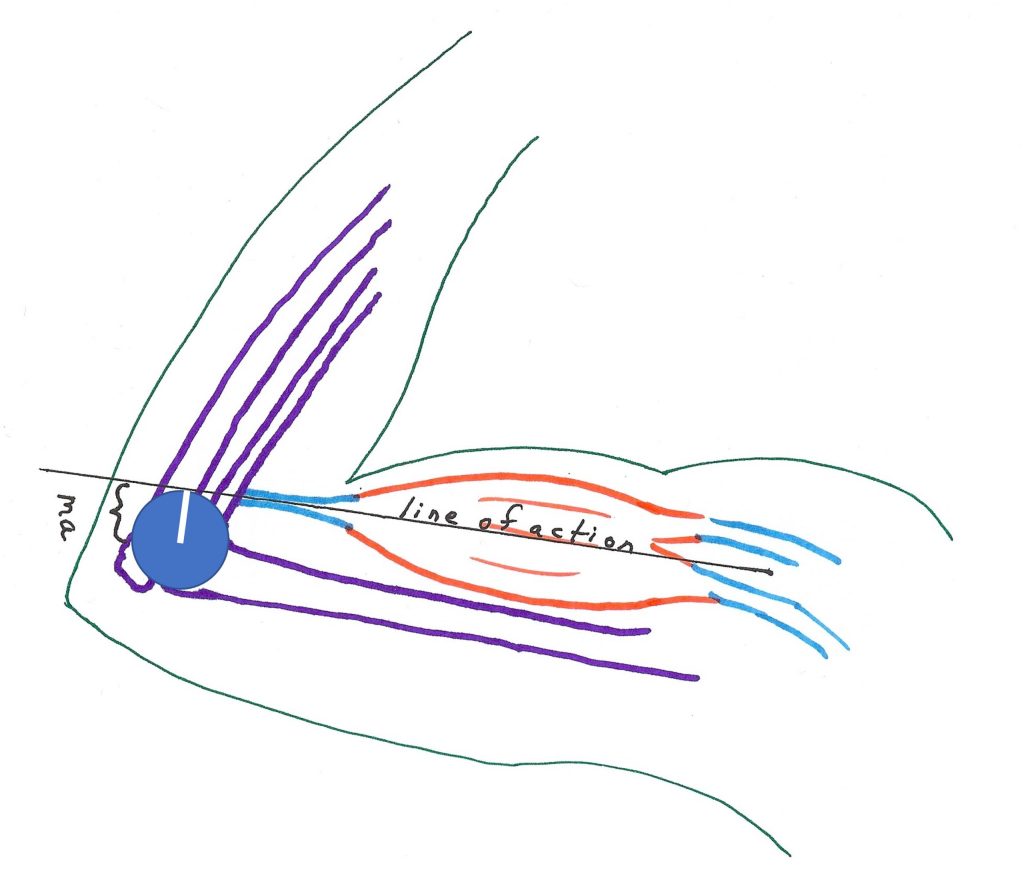
Our muscles are called “skeletal muscle” for a very good reason. In most cases, the skeletal muscles are connected at both ends to tendon that connects the muscle to bone. Our muscles function by exerting force against the bones, allowing movement, grasping, or posture. Adjacent bones form joints where motion occurs, so muscles exert a about the joint axis. A moment is a force exerted at some distance from the axis of rotation, resulting in the tendency for rotational motion. The moment about a joint is the force of contraction multiplied by the motor arm, the perpendicular distance from the centre of rotation of the joint to the line of action of the muscle-tendon unit (see Figure 5-3).
When muscle contracts, it can either generate force without length change, or generate force while changing length. The maximal force generated while not changing length is greatest at a middle length and is less at longer or shorter lengths. This is called the force-length relationship. When muscle shortens, the force decreases as velocity increases. This is called the force-velocity relationship. These properties of muscle are typically studied with maximal activation, but a graded muscle response is possible. The force of contraction of individual motor units can be graded by activation of motor units at progressively faster frequency of activation. This relates to the force-frequency relationship, which is actually dependent on the force-calcium relationship. The frequency of activation dictates the concentration of Ca2+ in the myoplasm; a higher frequency results in higher concentration of Ca2+. In addition to changing force by changing the frequency of activation (called rate coding), force can be graded by recruitment of more or fewer motor units.
Muscle is considered a “plastic” tissue; it has plasticity or adaptability. Muscle adapts to the demands we place on it. Muscles become stronger when we use them in more forceful movements and become less fatiguable when we use them often for endurance type exercise. Muscle also adapts in a negative manner, becoming smaller and weaker when we do not use them for forceful contractions and becoming less resistant to fatigue when we use them less often.
Astronauts can get by with minimal contraction of their muscles, so space travel results in atrophy unless countermeasures are taken.
Theories of Muscle Contraction
Early Theories of Muscle Contraction
Before we knew about the microscopic structure of muscle, it was difficult to explain how muscle contracted. The microscopic structure was just beginning to be understood in the mid 1950’s. So, when AV Hill proposed a new theory of muscle contraction in 1925, he was literally treating the muscle like a “black box” and trying to understand how it worked, based on observations he and others had made. At the time a dominant theory of muscle contraction was the surface tension theory. Although not clearly worked out, the general idea was that muscle contraction had something to do with surface tension; the tension generated at the surface between two substances generated by molecular interactions of like molecules unable to interact with the neighboring substance. Hill, who had conducted several experiments with isolated muscle as well as intact human subjects performing exercise, pointed out that surface tension decreases with increased temperature, but muscle force increases with increased temperature. However, he also pointed out that lactic acid was produced in proportion to force, even as temperature changed, so if lactic acid was involved in the surface tension generation, then it might be feasible.
Hill calculated the amount of lactic acid formed during a twitch contraction and estimated the surface of a “tube” of lactic acid formed within the muscle. His estimate of the surface tension thus created was way too small to account for the tension generated by the muscle. Therefore, he rejected the surface tension theory and proposed an alternative theory.
An Alternative Theory of Muscle Contraction
Hill was not satisfied to simply reject the current theory and not provide an alternative, so he formulated a potential mechanism for muscle contraction that he thought could generate the necessary force. His proposal included protein tubes with negative charge and clouds of positively charged ions around them. This alternating negative and positive charge would behave like an electronic condenser. The liberation of lactic acid somehow resulted in formation of sodium lactate and corresponding discharge of the condenser (Hill, 1928), allowing collapse of the system (shortening). This theory was certainly interesting, and creative, but had very little in terms of experimental support. A more generally accepted theory of contraction was that protein folding along the length of the fibre resulted in contraction. This also proved to be wrong. It was careful evaluation of microscopic images of muscle at different lengths that lead to the current theory of muscle contraction, the sliding filament theory.
Sliding Filament Theory of Muscle Contraction
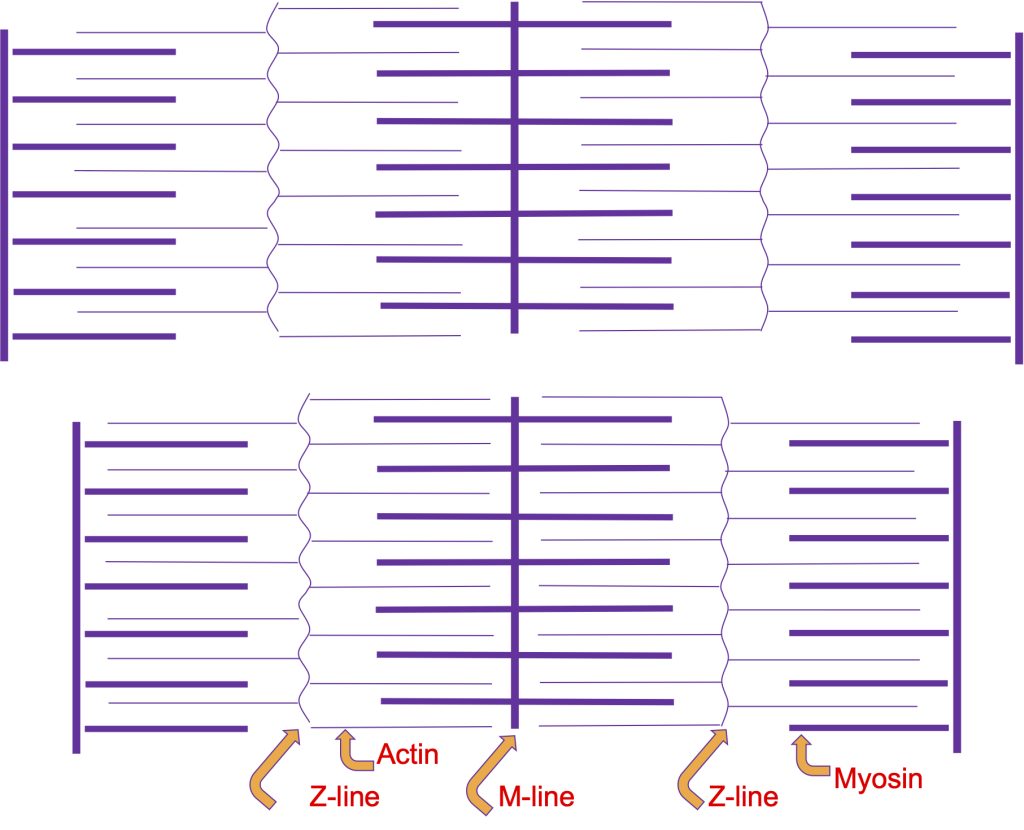
In the mid 50’s of the 20th Century, two Huxleys simultaneously proposed a theory of muscle contraction that has persisted to the current time (H. E. Huxley & Hanson, 1954). This theory dictates that striated muscle is structured in such a way that thick and thin filaments interdigitate longitudinally in intricately organized structures called sarcomeres. The middle of the sarcomere has parallel thick filaments that do not change in length as muscle length changes. Both ends of the sarcomere have thin filaments attached and projecting towards the middle, with some overlap of the thick and thin filaments. Thin filaments also do not change length when muscle shortens or is stretched.
Muscle changes length by interdigitation of thick (myosin) and thin (actin) filaments. The thin filaments slide past the thick filaments towards the middle of the sarcomere (see Figure 5-4). This is kind of like pushing two hairbrushes together, but with a double-sided hair brush in the middle, representing the myosin matrix. However, the sarcomere is much more organized than the hair-brushes would be (see Chapter 4 on Muscle Structure). The sliding filament theory of muscle contraction did not explain how this sliding occurred but did explain how length change was accomplished. The cross-bridge theory was needed to provide an explanation for force generation. The sliding filament theory, and cross-bridge theory, though not without contradiction (Pollack, 1983), are still generally accepted.
Cross-Bridge Theory of Muscle Contraction
In 1957, AF Huxley proposed his theory of muscle contraction that has come to be known as the cross-bridge theory of muscle contraction (A. F. Huxley, 1957). His elegant description of this theory provided an acceptable explanation for many of the known contractile and energetics properties of muscle. He proposed that during contraction, force is generated by projections or side-pieces of the thick filament that form cross-bridges to the thin filaments. We now recognize that these side-pieces are myosin heads and although the cross-bridge cycle is much better understood now, Huxley’s description and formulation of the cross-bridge theory is still accepted today. This theory and a description of the cross-bridge cycle follows.
The cross-bridge theory is based on the idea that myosin heads have some mobility about their attachment site on the thick filament. In the neutral position, the myosin head is not very likely to attach to actin, the adjacent thin filament. The probability of attaching to (this probability is denoted as f) and generating force is greater at some distance from the attachment site (towards the Z-disk). This function of the myosin head probably relates well with the notion that partial hydrolysis of results in a cocking of the myosin head, putting it in a position where it is more likely to attach to actin. It was proposed that each myosin head would function independently. Once the cross-bridge has been formed, there is a probability of detachment (denoted by g), and that probability rises to a high level if sliding of the thin filament relative to the thick filament is accomplished and the attachment site slides past the equilibrium point of the myosin head. Huxley also presented the idea that activation of contraction probably had something to do with making the binding sites on the thin filament available for binding with myosin. Without this availability, cross-bridge formation would not occur. This aspect of muscle control is further described below as part of excitation-contraction coupling. First, however, we will address the energy requiring processes associated with muscle contraction.
Energy Requiring Processes
The energy for muscle contraction comes from chemical energy in the terminal phosphate bond of ATP. The enzymes that are necessary for transducing the chemical energy to other forms of energy in muscle are classified as ATPase. Any form of ATPase will hydrolyze ATP, releasing the energy otherwise stored in the terminal phosphate bond, yielding ADP and inorganic phosphate (Pi). In particular, 3 such enzymes can account for most of the energy required during muscle contraction: actin-myosin-ATPase, sarcoendoplasmic reticulum ATPase (SERCA), and sodium-potassium ATPase (Na+K+ATPase). Each of these enzymes will now be discussed.

Actin-Myosin ATPase
The cross-bridge cycle (described below) is a series of reactions between the myosin head and the filament. This series of reactions involves, first of all, the free head of the myosin molecule partially hydrolyzing and using the energy to reconfigure to a structure referred to as the “cocked” or primed position. This configuration is considered a high-energy structure. When Ca2+ binds to troponin–C, the binding site on actin becomes exposed and the myosin head can bind to the actin filament. This binding is initially a weak binding, but the binding triggers the release of Pi, and the system transitions to a strong-binding configuration. The strong-binding state is also the stroke phase of the cross-bridge cycle. This transition generates force or movement and releases the energy that was originally in the ATP molecule. The cross-bridge cycle can generate work and also releases energy as heat. Each cycle of a cross-bridge uses one ATP molecule. Actin-myosin ATPase uses the majority of energy associated with muscle contraction.
SERCA
The pump that is responsible for maintaining intracellular [Ca2+] at a very low level (<90 nM) is also known as the sarcoendoplasmic reticulum Ca2+ATPase (SERCA). This pump is known as a uniporter because it transfers just one kind of ion (Ca2+) across a membrane in one direction. The density of SERCA on the surface of the sarcoplasmic reticulum is so high that there is little room for other proteins in this fenestrated organelle. Like most ion pumps, the energy needed to pump Ca2+ across the sarcoplasmic reticulum membrane is provided by ATP. For each hydrolyzed by this pump, two Ca2+ ions are transferred into the sarcoplasmic reticulum. The energy cost of transporting Ca2+ can account for up to 30% of the energy cost of muscle contraction. See the research highlight near the end of this chapter to see how this is experimentally determined. Any time ATP is split, there is some energy released as heat. This fact can explain the condition known as malignant hyperthermia (Gronert, 1980). Certain agents like halothane, a volatile anesthetic, can trigger widespread leak of Ca2+ from the sarcoplasmic reticulum, activating the SERCA and triggering actin-myosin ATPase activity. Due to the large rate of ion pumping throughout the body and cross-bridge cycling, and corresponding heat release, body temperature can rise to lethal levels. In spite of the fact that an antidote is available, halothane is no longer used for general anesthesia.
Sodium–Potassium ATPase
With each activation of a skeletal muscle fibre, some Na+ is transferred into the myocyte and some K+ is lost to the extracellular fluid. This ion transfer occurs through voltage-gated channels that briefly open, allowing Na+ and K+ to move down their electrochemical gradients. An increase in extracellular [K+] activates the Na+K+ATPase, and is hydrolyzed to provide the energy for ion pumping. This pump can transfer 3 Na+ ions and 2 K+ ions with each molecule of ATP hydrolyzed. The amount of ATP used by the Na+-K+ pump can account for up to 10% of the total energy cost of a muscle contraction.
Now that you understand the processes that require energy, it is time to learn how muscle is turned on. As we talk about the process of excitation-contraction coupling (E-CC), it is important to realize that these processes are initiated at all neuromuscular junctions where action potentials have been propagated. This could be very few in a small muscle that is not activated very vigorously, or literally millions of muscle fibres in a large leg muscle that is activated very vigorously.
Excitation-Contraction Coupling
Our muscles are organized in motor units; each fibre is activated by a single motoneuron. Muscles are activated by descending motor pathways that excite the motor nerves of a given muscle in the ventral horn of the spinal cord. Each cell body and the corresponding dendrites will have literally thousands of excitatory and inhibitory nerve endings contributing to or inhibition of the axon hillock, the location of the nerve cell body where the action potential originates. If the axon hillock reaches threshold, sodium and potassium channels will open and an action potential will be generated and propagated along the axon. Motor neurons are myelinated and conduction velocity is very fast (90-110 ms-1). When an action potential gets to the nerve terminals, the activation is transmitted to the muscle fibre by neuromuscular transmission, a process that results in generation of an action potential on the surface membrane of the muscle fibre, for each action potential arriving at the nerve terminal. The process of activating a skeletal muscle fibre, which includes several steps from generation and propagation of the action potential to mechanical engagement of myosin cross-bridges is a complex process, which will be described after the description of the process involved in neuromuscular transmission.
Neuromuscular Transmission
The process of neuromuscular transmission involves several steps from arrival of the action potential at the nerve terminal to generation of an action potential on the muscle membrane. It is important to realize that these steps will occur at all terminals of the same motoneuron, thereby simultaneously activating all muscle fibres of the motor unit. The number of fibres associated with each motor unit can vary from 10 or so to thousands. Each step in the process of neuromuscular transmission is described below.
Voltage-Gated Calcium Channels
Depolarization of the nerve terminal membrane with arrival of the action potential results in activation (opening) of a few voltage-gated Ca2+ channels. These channels open and allow Ca2+ to diffuse down its concentration gradient into the nerve terminal from the extracellular space. The result of just a few of these channels opening is that just a “puff” of Ca2+ comes into the nerve terminal, near each activated Ca2+ channel. This “puff” of Ca2+ is sufficient to trigger a sequence of events that result in emptying of a few vesicles into the synaptic cleft at each neuromuscular junction.
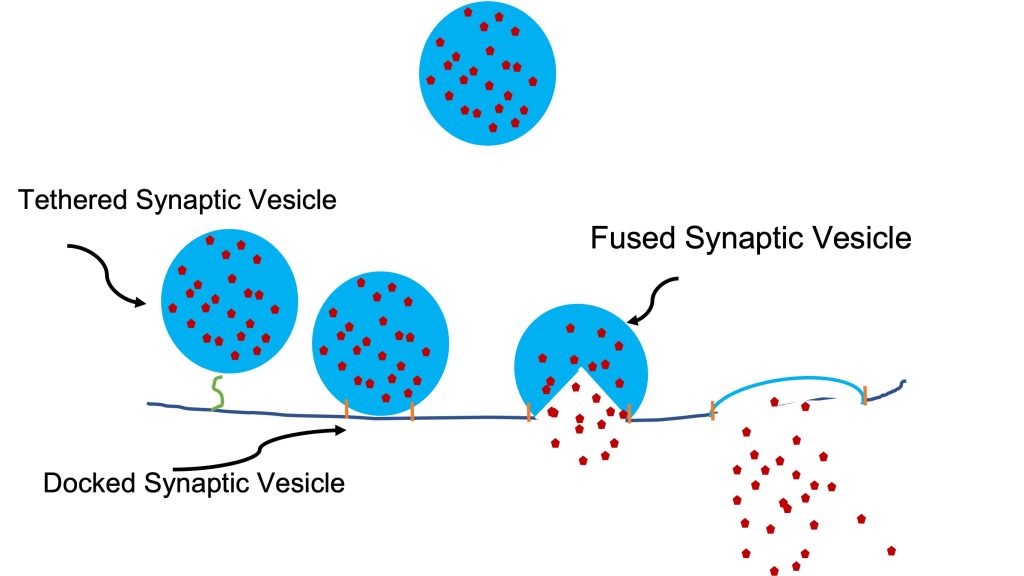
Fusion of Docked Vesicles
Vesicles within the nerve terminal contain acetylcholine. These vesicles are distributed such that some are freely floating throughout the nerve terminal, some are tethered close to the membrane across from the muscle and some are docked in this region. Vesicles have specialized proteins in their membrane that react with other specialized proteins in the nerve terminal membrane. Docking of the vesicle in this region is achieved by interaction of these special proteins. The local increase in [Ca2+] results in Ca2+ binding to one of these proteins that is part of the complex of proteins docking a synaptic vesicle to the nerve terminal membrane. This binding of Ca2+ triggers the fusion process; the vesicle membrane becomes nerve terminal membrane (exocytosis), essentially turning inside out and releasing acetylcholine into the synaptic cleft (see Figure 5-5). In a remarkable process of recycling, the membrane that was vesicle but is now part of the nerve terminal membrane can be reused to create a new vesicle. This preserves the specialized proteins needed in the vesicle membrane. The process of reforming the vesicle is called endocytosis.
Binding of Acetylcholine to its Receptors
Acetylcholine is the neurotransmitter of the neuromuscular junction. Once acetylcholine is released, it diffuses across the primary synaptic cleft and into the secondary synaptic clefts. On the postsynaptic membrane, there are specialized receptors for binding acetylcholine. In spite of the fact that only a few Ca2+ channels respond to depolarization of the nerve terminal, more than enough acetylcholine is released into the synaptic cleft to cause depolarization of the muscle end-plate region to threshold, resulting in generation of a muscle fibre action potential. This depolarization results from opening of a in the acetylcholine receptor that allows both Na+ and K+ to move across. Due to the fact that the electrochemical gradient for Na+ is stronger than for K+, more Na+ moves across the membrane than K+ and this causes depolarization. Once the depolarization reaches about -50 mV, voltage-gated Na+ and K+ channels open. These are the channels that are responsible for propagation of the action potential across the muscle membrane, spreading in all directions from the neuromuscular junction.
Destruction of Acetylcholine Terminates Neuromuscular Transmission
The neuromuscular junction gap is very confined. Acetylcholine diffuses in this confined area, and is captured by an enzyme “acetylcholinesterase” that splits acetate from the choline. Acetylcholinesterase is tethered to the basement membrane in the end-plate region. As the acetylcholine is split, its concentration will decrease and acetylcholine will be released from its receptor on the muscle surface. This terminates activation of the muscle. Nearly all of the acetylcholine that is released is deactivated by acetylcholinesterase; very little escapes to the surrounding area. Again, the neuromuscular junction has a fabulous recycling program. The choline is transported back into the nerve terminal where it is used to resynthesize new acetylcholine. The recycled vesicles are resupplied with new acetylcholine.
Muscle Membrane Response
An action potential is generated on the muscle plasmalemma, similar to the action potential on an axon. Membrane voltage quickly changes from -85 mV to +20 mV then repolarizes to the normal resting membrane potential. For each axon action potential, there is a muscle fibre action potential that is propagated over the surface membrane of the myocyte at a rate of 2-5 m⋅s-1. This is quite slow in comparison with a motor axon conduction velocity (~100 m⋅s-1). The action potential is also conducted into the muscle fibre via the transverse-tubules. The transverse tubules are continuations of extracellular environment into the muscle fibres and encircle the myofibrils. The transverse-tubules are located at regular intervals along the muscle fibre, allowing activation of each sarcomere near the A-I junction. It appears that the transverse-tubules stay approximately 500 nm from the Z-disk as sarcomere length changes (Brown & Loeb, 1999).
There is no energy cost linked directly to the generation and propagation of the action potential. The ions Na+ and K+ move down their electrochemical gradient when the voltage-gated channels open. However, to preserve the ion concentration gradients, it is necessary to pump these ions back to where they originated; Na+ is pumped out of the myocyte and K+ is returned from the extracellular space to the cytoplasm. This active transport is achieved by Na+K+ATPase, a transporter that uses energy from to transfer 3 Na+ and 2 K+ with hydrolysis of each ATP molecule.
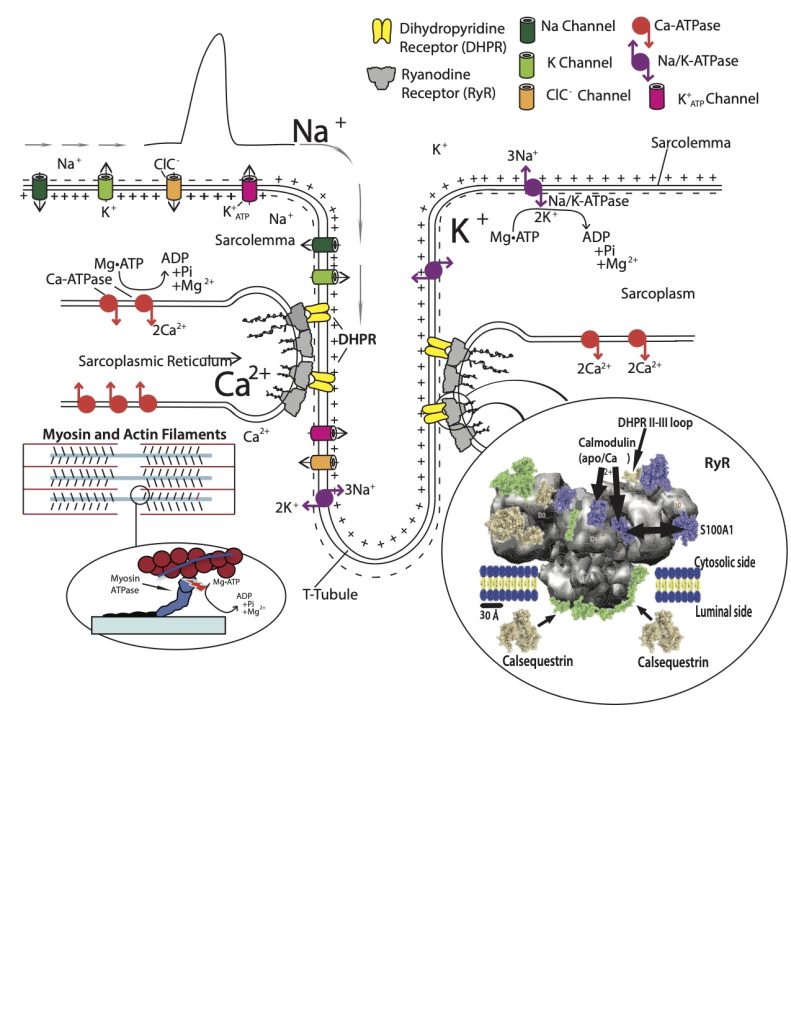
Internal Membrane Potentials
The transverse-tubules are continuations of the sarcolemma that go deep into the myocyte, encircling the myofibrils about 500 nm from the Z-disk. The surface action potential is propagated into the transverse-tubules. In addition to the Na+ and K+ channels in the sarcolemma of the transverse-tubules, this membrane also has receptors (DHPR) which function as voltage detectors. DHPR are actually modified Ca2+ channels, that do not require Ca2+ to go through them to serve the function of activating skeletal muscle. Half of the DHPR are linked directly to ryanodine receptors (RYR) which are actually embedded in the membrane of the terminal cisternae, the enlarged portion of the sarcoplasmic reticulum that lies adjacent to the transverse-tubule. The proximity of the terminal cisternae on either side of the transverse-tubule in cell cross-sections as a repeating structure of three membrane bound structures has been given the name of “triad”. This structure is evident in Figure 5-6 where the grey ryanodine receptors are adjacent to the transverse tubule.
Calcium Handling in the Muscle Cell
When the DHPR detects the membrane potential change associated with the action potential, they trigger the opening of the RYR to allow Ca2+ to move down its concentration gradient from the terminal cisternae into the sarcoplasm. Although this event (Ca2+ release) is happening at the sarcomere level of a myofibril, this occurs throughout the myocyte as the action potential is moving across the surface membrane and into all of the transverse tubules. The amount of Ca2+ released from the sarcoplasmic reticulum with each activation (action potential) is sufficient to raise the myoplasmic [Ca2+] from the resting value of 70 nM to 200 µM. However, the actual increase in free [Ca2+] with a single release event like this is less than 1 µM. The reason for this huge discrepancy is that much of the released Ca2+ binds immediately to a number of Ca2+ buffers in the myoplasm. These buffers include: ATP, calmodulin, SERCA, parvalbumin, and troponin–C.
The rise and fall of [Ca2+] in the myoplasm is called the calcium transient. In response to a single activation, this calcium transient is very brief; it is over in a few milliseconds. However, when several activations occur in quick succession, the cumulation of calcium transients can result in a sustained elevation of [Ca2+].
The buffering of Ca2+ by these molecules often has subsequent consequences. For example, binding of Ca2+ to calmodulin activates a number of enzymes, like myosin light chain kinase. This topic is further discussed in the chapter on Repetitive Contractions (see Chapter 12). Binding of Ca2+ to SERCA,results in transfer of Ca2+ into the sarcoplasmic reticulum, allowing further binding of Ca2+ and decreasing myoplasmic [Ca2+]. Binding of Ca2+ to troponin-C is the event that activates muscle contraction.
Troponin and Tropomyosin
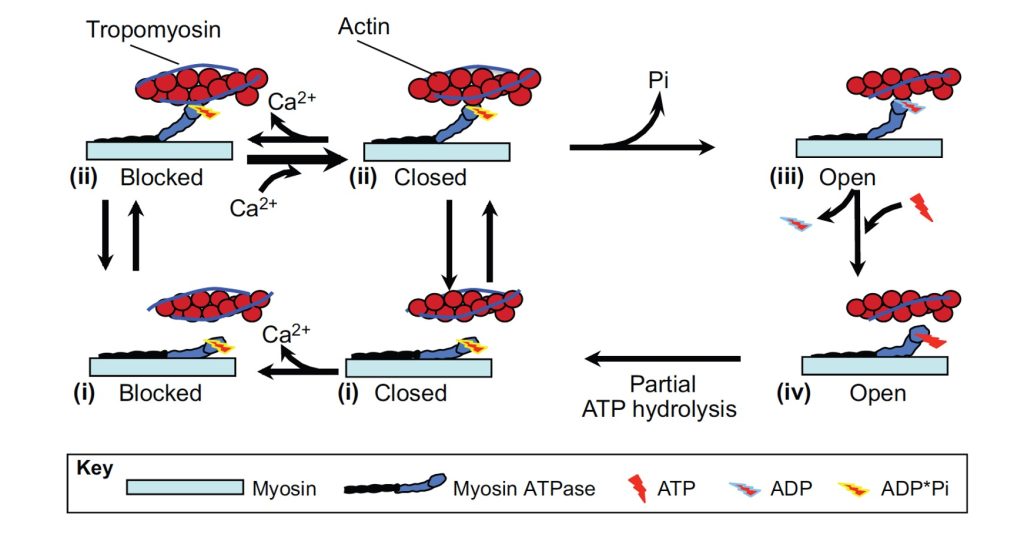
Troponin-C is a Ca2+-binding protein, part of the troponin complex (Troponin-C, -I, and -T) associated with tropomyosin and the thin filament of the sarcomere (see Figure 5-7). The thin filament is composed mostly of actin. Each tropomyosin molecule spans 7 filaments, lying over the myosin-binding site. This position blocks binding of myosin to actin. Binding of Ca2+ to troponin-C causes a realignment of this protein complex such that tropomyosin is pulled out of the groove between the two strands, exposing the binding site for myosin on actin. This allows the crossbridge cycle to be initiated. The crossbridge cycle will continue as long as Ca2+ is bound to troponin-C.
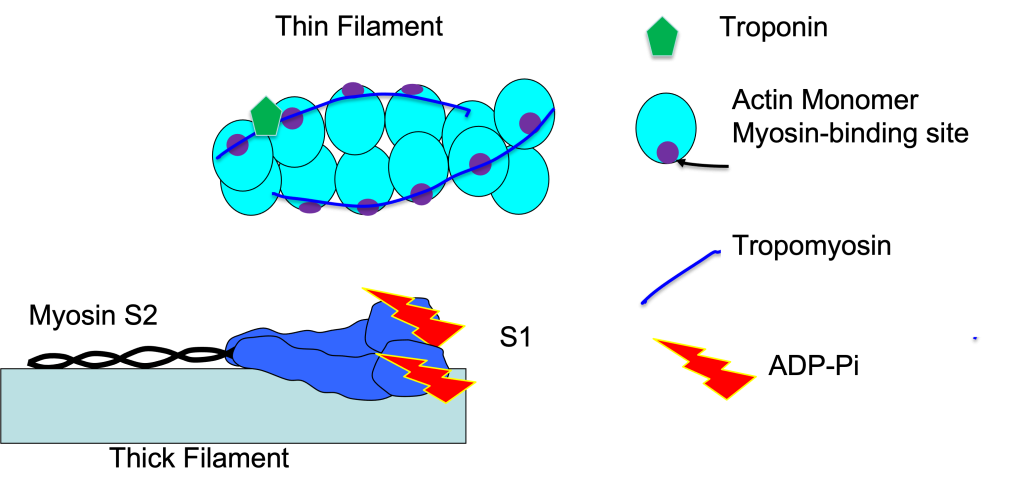
Crossbridge Cycle
The exposure of the binding site for myosin on the filament permits binding of the myosin head to actin, creating a crossbridge. The initial binding of the myosin head to actin is considered a weak-binding state. Once the crossbridge is formed, Pi is ejected from the myosin head and this reaction allows change to the strong-binding state. This transition is also called the power-stroke. The crossbridge maintains this force generating position until it disengages. Disengagement of the crossbridge results from the probability of dissociation (g), which increases to a high level if length change is associated with this crossbridge activity. This letting go requires release of ADP and binding of a molecule of . The binding of ATP to the myosin head allows disengagement of the crossbridge. The free myosin head now partially splits ATP to ADPPi. This partial splitting causes a structural rearrangement of the myosin head to the cocked position, a structure that can undergo the stroke, once it is again bound to actin. If the binding site on the actin filament is still available, this now cocked myosin head can bind and undergo another cycle. Cycling of the crossbridge will continue as long as Ca2+ is bound to troponin-C. See Figure 5-8.
The collective effect of crossbridge cycling is that force is generated, and movement is possible. Force will be generated by each crossbridge that binds to actin. Total active force will be proportional to the number of crossbridges bound in parallel (across all parallel sarcomeres). The same force must be generated in all sarcomeres in series. If the resistance to shortening is sufficient, no length change will occur. Once the force generated by the crossbridges exceeds the resistance, shortening will occur. If the load on the muscle exceeds the force generated by the crossbridges, lengthening occurs.
Asynchronous Motor Unit Activation
The frequency of action potentials on the motor nerve dictates the frequency of action potentials on the muscle membrane because there is a one-to-one relationship between nerve and muscle action potentials. However, in a voluntary contraction, motor unit activation is asynchronous so the oscillations seen at subfusion frequencies are lost in a smoothing effect of activation of multiple motor units.
Types of Contraction
When a muscle is activated, crossbridge cycles are initiated, and force develops. The type of contraction is called fixed-end if the muscle-tendon length does not change. A truly isometric contraction occurs without muscle fibre length change. However, these two terms (fixed end contraction and isometric contraction) are sometimes used interchangeably. Often, the term isometric will be used to describe a contraction that does not have length change of the muscle-tendon unit. The muscle-tendon unit will shorten if the load on the muscle is not sufficient to prevent shortening or it will lengthen if the load exceeds the force generated by the muscle. When length change occurs, the contraction is called dynamic. The term “auxotonic” has also been used to describe muscle contraction where the force changes through-out the duration of the contraction and some fibre shortening occurs. A special form of dynamic contraction is one where the velocity of shortening is controlled. This is an isokinetic contraction.
Active and Passive Force and Types of Contraction
When you stretch an inactive muscle, it resists the stretch with a small force that is independent of activation, but this passive force increases with length. This is called passive force and is the property of passive structures like connective tissue, membrane, and titin. When a muscle is activated, crossbridge cycles are initiated, and the force increases above the passive force. In general, muscle physiologists calculate the active force by subtracting the passive from the peak force. This calculation assumes that passive force remains constant during the contraction, and that active force simply adds to the passive force. However, it has been shown that passive force most likely decreases while active force is increasing (MacIntosh & MacNaughton, 2005). This happens because the tendon is stretched slightly as active force develops and the muscle fascicles decrease in length, decreasing the passive force across these passive structures.
Active force is calculated by subtracting the appropriate passive force from the peak force reached during a contraction (MacIntosh & MacNaughton, 2005). This should represent the actual force generated by energy-requiring processes (crossbridge cycling). The way of calculating active force is illustrated in Figure 5-9. The active force achieved by a given stimulation is dependent on several factors including frequency of activation, [Ca2+], sarcomere length, and velocity of length change.
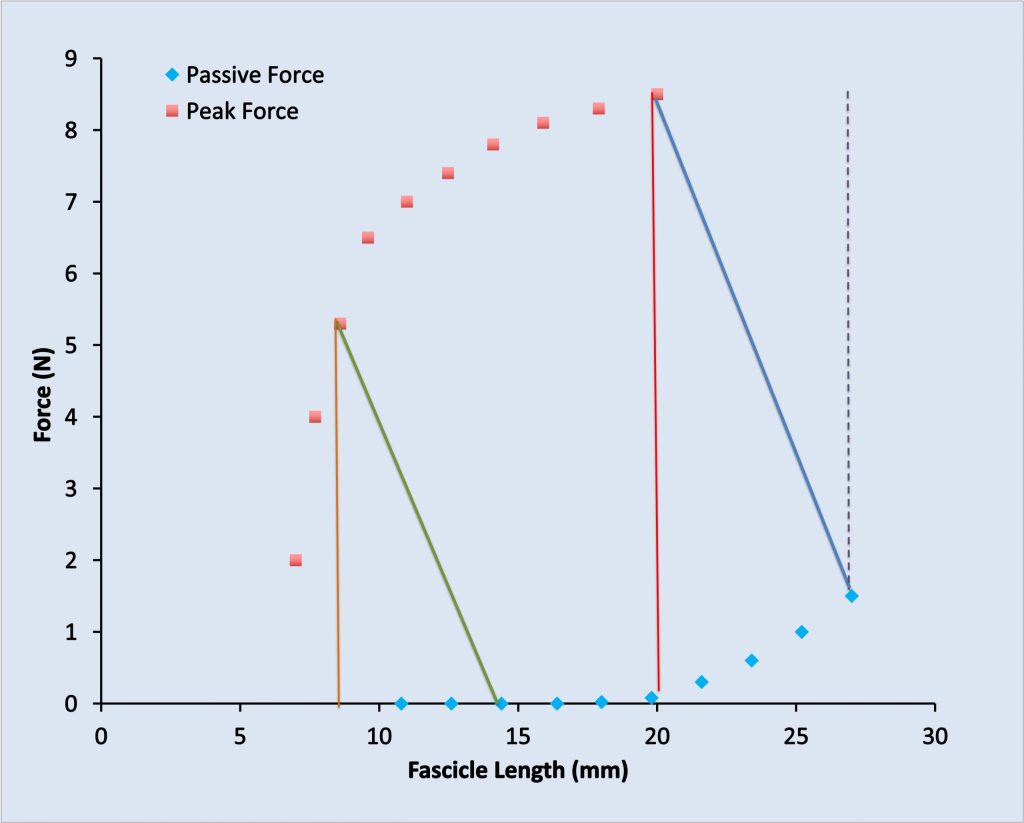
This graph shows passive (blue diamonds) and peak (brown squares) force for a series of tetanic contractions of the rat medial gastrocnemius muscle obtained at different lengths. The blue diamonds show initial force for each contraction and the brown squares show peak force. Active force is calculated by subtracting the passive force from the peak force. Often, this is done by subtracting the passive force measured prior to the contraction, as indicated by the vertical dashed line. The correct way to calculate active force is to subtract the passive force that would be expected at the fascicle length reached at the peak of contraction as shown with the vertical red line. When the initial passive force is zero, the passive force before the contraction is the same as the passive force expected at the peak of the contraction. This is shown with the light brown line.
The Isometric Contractile Response
Activation of a muscle results in a contractile response that is dependent on the number and frequency of action potentials propagated across the surface membrane. With each activation, [Ca2+] rises and falls, but with increasing frequency, the average [Ca2+] achieved will be higher. The voluntary frequency of activation of human muscle is in the range of 8 Hz to 70 Hz, except for brief doublets or triplets (2-3 activations) at higher frequencies, often associated with initiation of ballistic contractions. The response to a single activation is called a twitch contraction while the response to repeated activations without complete relaxation between activations is known as a tetanic contraction.
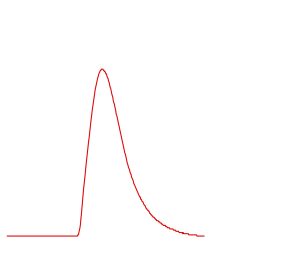
Twitch Contraction
The rise and fall of active force during a twitch contraction is an elegant contractile response to a single activation (see Figure 5-10). The amplitude of force response depends on several factors, including: sarcomere length, temperature, prior activation ( and activity dependent potentiation) as well as cross-sectional area of the cell, motor unit, or muscle stimulated. The term “twitch” is sometimes used to describe the contractile response to a doublet (two pulses) stimulation when the frequency is high. This alternative use of the term can only be understood by the context of the use, something the learner in exercise physiology needs to be aware of.
Tetanic Contraction
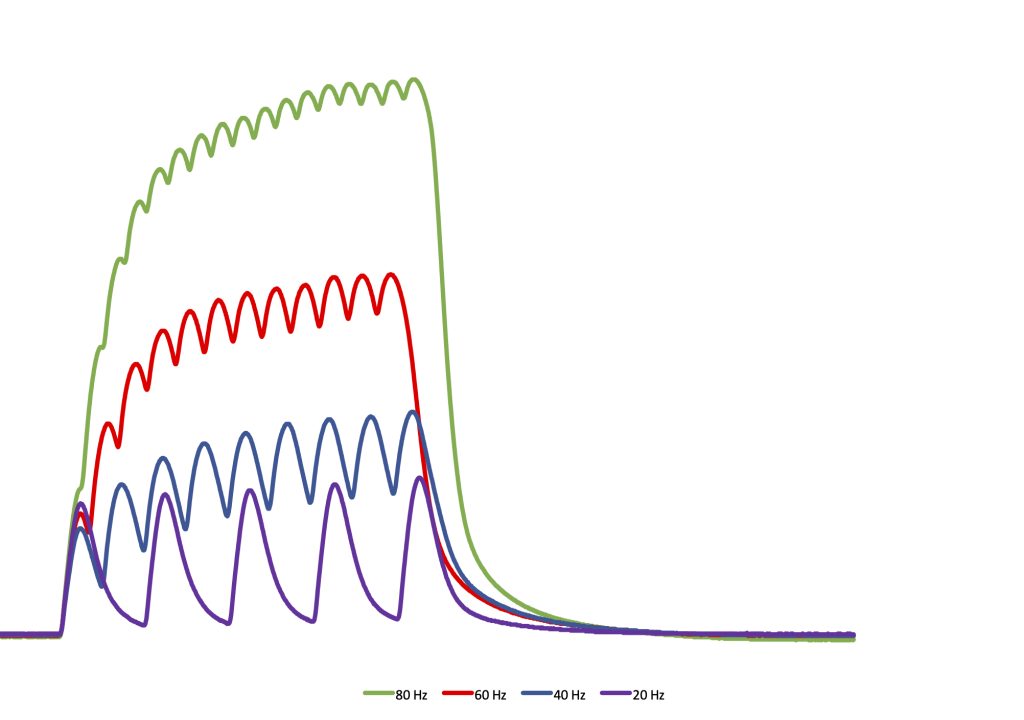
When more than one activation is given and the interval between activations is within the time of the twitch contraction, summation occurs. That is, force will begin to rise again before relaxation is complete, like adding subsequent twitch contractions to what is already there. If oscillations of force are evident during repetitive activation, then this contraction is referred to as an incompletely fused tetanic contraction (Figure 5-11). If no oscillation of force is detected with each activation, then it is a completely fused tetanic contraction (Figure 5-12). The amount of relaxation between sequential activations depends on several factors: fibre-type, species, temperature, and sarcomere length.
Incompletely Fused Tetanic Contractions
The relationship between frequency of activation and active force is shown in Figure 5-13. When a muscle is activated at a very low frequency, independent twitch contractions will result. When sequential activations are delivered closer together, eventually an activation will arrive before complete relaxation has occurred. Now fusion occurs; first incomplete then complete as the frequency of activation increases. As frequency of activation increases, the average myoplasmic [Ca2+] will increase. With higher myoplasmic [Ca2+] active force will be higher, according to the force-Ca2+ relationship (see Figure 5-14).
Completely Fused Tetanic Contractions
When sequential activations occur with a short interval, such that no relaxation is permitted between activations, the contraction is called a completely fused tetanic contraction. This complete fusion typically occurs near maximal active force.
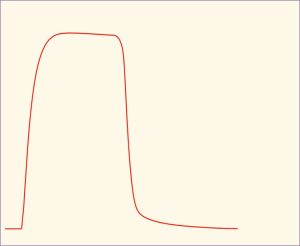
Dynamic Contractions
Muscle contraction is a process that is triggered by binding of Ca2+ to troponin. The amount of Ca2+ that binds to troponin depends on motor unit recruitment (how many motor units are activated) and rate coding (frequency of activation of each motor unit). The consequence of muscle contraction is one of the following: shortening, lengthening, no change in length or stretch-shortening or shortening-stretch. One of the interesting and common types of contraction is the stretch-shortening contraction (Komi & Nicol, 2000). This is also known as a ballistic contraction where motion in one direction is slowed then reversed by contraction of the agonist for the shortening motion. For example, we often jump with a stretch-shortening contraction of our quadriceps muscles. The jump motion is preceded by a drop. We contract our quadriceps muscles to slow the drop, which is achieved with lengthening of these muscles and activate them more to accelerate upwards which requires shortening of the quadriceps muscles.
Fundamental Contractile Properties of Skeletal Muscle
The force of skeletal muscle contraction can be considered to be modulated by several fundamental factors: calcium concentration or frequency of activation, sarcomere length, and velocity of shortening. Each of these fundamental properties of muscle will be described here. In addition, the force response is dependent on the history of activation. Potentiation and fatigue, resulting from prior activation, are presented in the Chapter on “Repetitive Muscle Activation” (see Chapter 12).
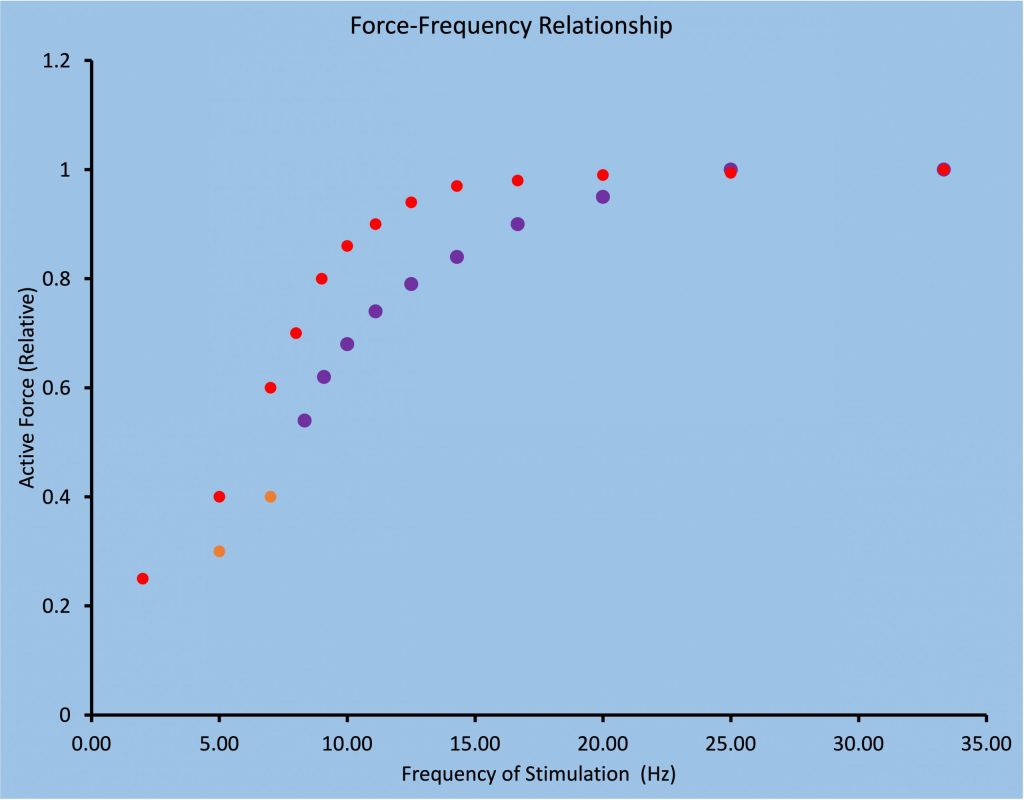
Force-Frequency Relationship
Individual twitch contractions have an active force that is typically 10-30% of the maximal active force obtained with a completely fused tetanic contraction. Keeping in mind that muscles are activated by action potentials on motor nerves, the frequency of activation of a motor unit depends on the frequency of activation on the corresponding motor neuron. Frequency is the inverse of interval between sequential activations. Typically, human motor units are activated initially at about 8 Hz, and a brief contraction may have a train of 6-20 action potentials. Frequency of activation is often presented as an average because the actual interval between activations varies somewhat from one interval to the next.
As intensity of contraction increases, the frequency of activation increases, up to 60 to 80 Hz for sustained frequency. However, there is sometimes a higher frequency for the initial two or three activations for ballistic contractions. Higher frequency means more fusion and higher active force. Figure 5-14 shows the relationship between frequency of activation and active force for a maximally activated whole muscle of mixed fibre-type composition. Typically, a slow-twitch motor unit will have fusion at a lower frequency; a completely fused contraction will occur at a lower frequency. A fast-twitch motor unit will require a higher frequency of activation for complete fusion. The relationship between active force and frequency of activation is shifted to the left for slow-twitch motor units and to the right for fast-twitch motor units. Since slow-twitch motor units are typically smaller than fast-twitch motor units, the peak active force for slow-twitch motor units will be less than peak active force for fast-twitch motor units.
The frequency of activation will determine the average [Ca2+] in the myoplasm during the contraction. This concentration dictates the amount of binding to troponin-C. The binding of Ca2+ to troponin-C determines the number of crossbridges that are cycling. Therefore, the force-frequency relationship is closely linked to the force-calcium relationship. The relationship between frequency of activation and force is a sigmoidal relationship as seen in Figure 5-14.
Force-pCa2+ Relationship
As described above, muscle contraction is turned on by the release of Ca2+ into the myoplasm. The free [Ca2+] determines what proportion of available troponin C has Ca2+ bound to it, and this binding allows crossbridge attachment and force generation along the adjacent thin filament. This same sequence of Ca2+ release, diffusion, and binding will occur simultaneously all along each activated muscle fibre. The force exerted by the muscle will depend on how many motor units are activated and the average [Ca2+] in those activated muscle fibres. The [Ca2+] depends on the frequency of activation within a contraction. This combination of recruitment and frequency of stimulation allow fine control over the force generated by a muscle.
The force-calcium relationship is typically quantified in a skinned fibre preparation (Stephenson, 1981; Wendt & Stephenson, 1983). With this approach, [Ca2+] can be regulated carefully and force can be allowed to reach a plateau. Alternatively, the force-Ca2+ relationship can be determined in intact single muscle fibres with stimulation and measurement of both [Ca2+] and force (Balnave & Allen, 1995; Glass, Cheng, & MacIntosh, 2018). The relationship between force generated by the muscle and [Ca2+] obtained in this way is shown in Figure 5-15. It can be seen that the relationship is sigmoidal. At very low [Ca2+], no active force is generated, though there may be passive force if the muscle is at a long length. At progressively increasing [Ca2+] active force is progressively greater. The increase is small at low concentrations, but the increase in active force for a given increase in [Ca2+] is greater through the middle range, then the slope decreases and active force reaches a plateau where further increases in [Ca2+] result in no further increase in active force. The graph shows a discreet active force for any [Ca2+]. However, the position of the line of the graph can be modulated. Several factors increase or decrease Ca2+ sensitivity . When Ca2+ sensitivity increases, the curve is to the left. There is more force at any given submaximal [Ca2+]. When Ca2+ sensitivity decreases, the curve shifts to the right. There is less force at any given submaximal [Ca2+]. Maximum force is not altered by Ca2+ sensitivity. The [Ca2+] that results in half the maximal force is a measure of Ca2+ sensitivity. As sensitivity increases, the half-maximal [Ca2+] decreases.
![By Brian R. MacIntosh This graph plots relative force (varying between 0 and 1.0 against miocromolar [Ca2+], ranging from 0 on the left to 1.2 on the right. Two lines rise from the baseline to a plateau with a sigmoidal shape. The control line is the top one. Contractile force increases sigmoidally as [Ca2+] increases. The line on the right begins to rise at the same [Ca2+], but the slope is less and it rises to a lower plateau. This represents fatigued muscle where the Ca2+ sensitivity is decreased and the maximum force is decreased, probably due to less force per cross-bridge.](https://pressbooks.openeducationalberta.ca/app/uploads/sites/228/2023/01/fig5-14-.jpg)
The known factors that influence calcium sensitivity include the following:
- sarcomere length
- pH
- regulatory light chain phosphorylation
- temperature
- [Pi]
There are two potential mechanisms for altering the force at a given submaximal [Ca2+] by which these cellular changes alter calcium sensitivity (MacIntosh, 2003). The predominant mechanism is related to affecting crossbridge kinetics, but it is also possible that binding of Ca2+ to troponin can be altered. This would certainly alter the magnitude of force of contraction at a given [Ca2+].
Muscle Length and Ca2+ Sensitivity
When sarcomere length is changed, the diameter of the cell and of individual myofibrils changes. With increased sarcomere length, the myofilament lattice is compressed. With decreased sarcomere length, the myofilament lattice expands. This means at long lengths the myofilaments are close together and at short lengths there is more distance between the filaments. Increasing sarcomere length increases calcium sensitivity because the myosin heads are brought closer to the filaments, increasing the probability of crossbridge formation. When this approach is used with skinned fibres, the myofilament lattice can be ‘shrunk’ with addition of dextran (Wang & Fuchs, 2000) to the solution in which the muscle was immersed. Shrinking the myofilament lattice in this way increases Ca2+ sensitivity, confirming that it is the dimensions of the myofilament lattice that influence the length dependence of Ca2+ sensitivity.
pH and Ca2+ Sensitivity
Early reports of changes in Ca2+ sensitivity and were interpreted as evidence that acidosis contributes to decreased contractile response known as fatigue. Fabiato and Fabiato (1978) demonstrated that when pH was decreased from 7.4 to 6.2, both Ca2+ sensitivity and maximal force were decreased. These authors also demonstrated that the mechanisms for the inhibitory effect of acidosis was not related to competitive binding of Ca2+ with troponin. They suggest the mechanism had something to do with a step in the contractile process after binding of Ca2+ to troponin. These experiments were conducted on mechanically skinned frog muscle fibres at 22ºC. The impact of this research was profound. Essentially a primary mechanism of had been found. The notion that acidosis was a primary factor in muscle fatigue persisted until 1995 when it was shown that the effectiveness of acidosis to decrease Ca2+ sensitivity was diminished when muscle was tested at 30ºC (Pate, Bhimani, Franks-Skiba, & Cooke, 1995). This result suggests that at physiological temperatures, acidosis has very little impact on fatigue of skeletal muscle. It has been demonstrated that in alkalotic solutions, the myosin heads are more scattered, having greater mobility than in acidosis where the myosin heads are uniformly pressed against the thick filaments (Podlubnaya, Kakol, Moczarska, Stepkowski, & Udaltsov, 1999). This mobility of the myosin heads is thought to contribute to increased Ca2+ sensitivity by bringing the myosin heads in close proximity to the filaments, similar to the mechanism proposed for myosin light chain phosphorylation.
Regulatory Light Chain Phosphorylation and Ca2+ Sensitivity
Skeletal muscle myosin contains two light chains, one called essential, and one referred to as regulatory. The essential light chain is necessary for actin-myosin-ATPase activity (Harrington & Rodgers, 1984). The regulatory light chain can be phosphorylated and this phosphorylation results in increased Ca2+ sensitivity (Persechini, Stull, & Cooke, 1985). Repeated activation of skeletal muscle results in activation of myosin light chain kinase and this enzyme phosphorylates the regulatory light chain. Activity dependent potentiation is correlated with magnitude of light chain phosphorylation (Moore & Stull, 1984). The mechanism by which Ca2+ sensitivity is increased by regulatory light chain phosphorylation is similar to the mechanism associated with pH. Without light chain phosphorylation, the myosin heads lie close to the thick filament backbone. When the light chains are phosphorylated, the swing free with increased mobility (Levine, Kensler, Yang, Stull, & Sweeney, 1996). This increased mobility corresponds with increased probability of myosin head interaction with actin and crossbridge formation; more force is obtained at a given submaximal [Ca2+]. The increased probability of crossbridge formation results in a faster rate of rise of force (Sale, 2002).
Temperature and Ca2+ Sensitivity
Mammalian muscle operates at temperatures ranging from 30ºC to 40ºC. In this temperature range, Ca2+ sensitivity is low. When muscle is cooled, as is often the case when it is studied in vitro, Ca2+ sensitivity increases. It is thought that the mechanism by which Ca2+ sensitivity is altered by temperature is similar to the mechanisms for regulatory light chain phosphorylation and pH. Decreasing temperature causes the myosin heads to increase mobility, swinging away from the thick filament back-bone. Increasing temperature has the opposite effect. When the myosin heads have increased mobility, they have a greater probability of binding to actin, forming crossbridges and generating force. It should be noted that along with changing Ca2+ sensitivity, muscle temperature has other effects as well. For example, increasing temperature will increase the force per crossbridge, and maximal velocity. This effect of temperature is an important aspect of warm-up because output is improved across a range of velocities.
Inorganic Phosphate and Ca2+ Sensitivity
During repeated contractions, inorganic phosphate (Pi) accumulates due to the net breakdown of creatine phosphate. The concentration of Pi can increase from a few mM to 20-30 mM. An important step in the crossbridge cycle is the release of Pi. This step allows transition to the force-generating stage of the cycle. Increased [Pi] slows the release of Pi, slowing the transition to force generation. This means there will be less force at a given [Ca2+] than would otherwise be expected; Ca2+ sensitivity is decreased. Maximal force is also decreased by Pi.
Interaction Among Factors Affecting Ca2+ Sensitivity
It is apparent when reading through the descriptions for mechanism of changes in Ca2+ sensitivity that there is a common theme. Proximity of the myosin heads to improves Ca2+ sensitivity. This is achieved with any of the following mechanisms:
- osmotic compression in skinned fibres
- increased sarcomere length
- increase
- decreased temperature
- increased regulatory light chain phosphorylation.
It should not come as any surprise that if you increase the mobility of the myosin heads by one mechanism, then other factors that operate by this mechanism become ineffective. For example, regulatory light chain phosphorylation is not very effective at increasing Ca2+ sensitivity at low temperature (room temperature or lower), or at long sarcomere length (Rassier & MacIntosh, 2002). Similarly, at warm temperature where myosin head mobility is already decreased, decreasing pH has little impact. These interactions are described further by MacIntosh (2003).
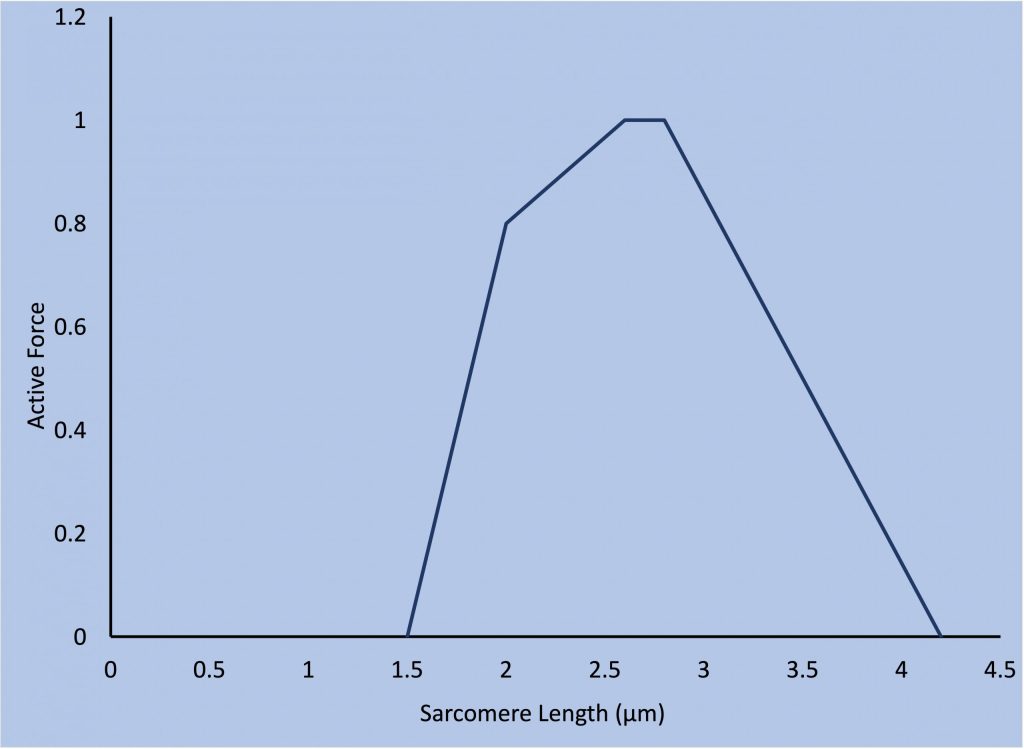
Force-Length Relationship and the Length Dependence of Force
The force-length relationship relates sarcomere length to maximal active isometric force and passive force of muscle. Passive force is typically zero until sarcomere length reaches the optimal length for peak active force. At this length or slightly longer, passive force will rise as length increases (see Figure 5-15). Maximal active force is very low at short sarcomere lengths and increases to a peak at a sarcomere length that allows the greatest overlap of thick and thin filaments (Gordon, Huxley, & Julian, 1966). This is the ascending limb of the force-length relationship. Myosin filaments are universally 1.6 µm in length, but (thin) filaments vary according to species. Human actin filaments are about 1.3 µm in length, so optimal sarcomere length (plateau) ranges from 2.6 µm to 2.8 µm. Beyond this sarcomere length, overlap decreases, so maximal force also decreases (Rassier, MacIntosh, & Herzog, 1999). This is the descending limb of the force-length relationship. If overlap decreased to zero, it would be expected that active force would be zero. In human muscle, this should happen at a sarcomere length of 4.2 µm. It seems unlikely that sarcomere length could reach this extreme, but it has been reported to occur (Lieber, Loren, & Friden, 1994).
Although it is easy to understand why active force is greatest on the plateau where overlap of the myofilaments is greatest, and active force decreases linearly at longer sarcomere lengths, the factors affecting active force on the ascending limb of the force-length relationship are more complicated. Several factors appear to contribute to this property of muscle. When sarcomere length decreases below the length associated with the length of two thin filaments, then the thin filaments must overlap with each other in the middle of the sarcomere. It is possible that this results in interference with the appropriate actin-myosin interaction. Thin filaments from the wrong end of the sarcomere may bind inappropriately with some myosin molecules. This overlap increases as sarcomere length decreases, increasing the likelihood of such interference. In addition, when the sarcomere length is no longer than the myosin filament (1.6 µm), the thick filaments will press against the Z-disks. This interaction of myofilaments with intermediate filaments may detract from generation of active force.
Submaximal Activation and the Length Dependence of Active Force
When activation of a muscle is submaximal (according to the force-frequency or force-pCa2+ relationship), the relationship between sarcomere length and submaximal active force is referred to as the length dependence of force. The active force still has an ascending limb, a plateau, and a descending limb. However, the plateau for submaximal contractions is shifted to the right. This indicates that some factor in addition to overlap of myofilaments has an influence on Muscle Blood Flow and Oxygenation. The Moxy monitor outputs two variables, the total hemoglobin (tHb) which reflects changes in microvascular blood volume 30, and the muscle oxygen saturation (SmO2), which reflects the ratio of the oxygenated hemoglobin and myoglobin to the total hemoglobin and myoglobin and is suggested to indicate the balance between muscle oxygen delivery and utilization 30. During high-intensity isometric contractions, SmO2 will tend to decline as the muscle rate of oxygen utilization exceeds its rate of delivery, while during the rest periods, the trend is reversed, creating a “sawtooth” pattern during an intermittent isometric test. As it has been shown to be more reliable than comparing more discrete time points 31, the change in SmO2 during the contractions (∆SmO2-work) and during the rest periods (∆SmO2-rest) were averaged across all contractions and compared between conditions when activation is submaximal. This additional factor appears to be Ca2+ sensitivity (MacIntosh, 2017) and the property of muscle that causes this shift of optimal length is called length dependent activation. One of the key factors affecting the active force at a given submaximal [Ca2+] is proximity of the myosin head to the binding site on filaments (MacIntosh, 2003). As muscle length increases, the distance between filaments decreases. This makes it easier for crossbridge formation, so myosin heads bind more quickly, increasing the rate of force development.
Force-Velocity and Power–Velocity Relationships
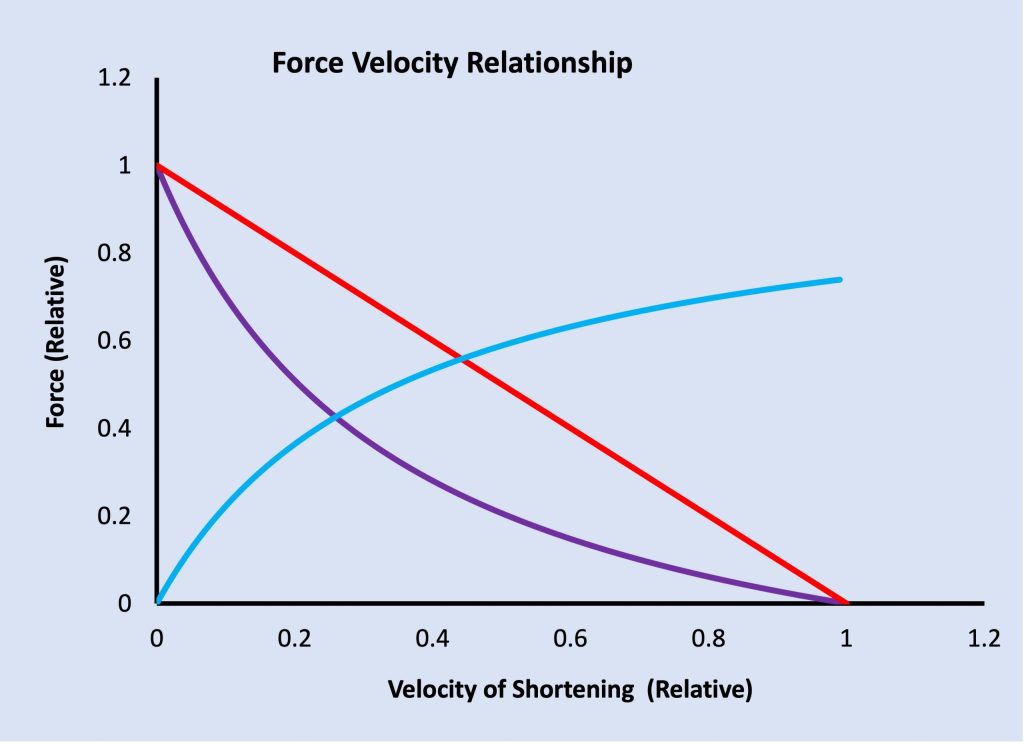
The relationship between active force and length described above relates entirely to isometric contractions. When the muscle length is allowed to change during the contraction, the force exerted by individual crossbridges will change, depending on whether length is increasing or decreasing. The force-velocity relationship describes the decrease in active force as the rate of shortening increases (see Figure 5-16). This relationship shows that as velocity of shortening increases, the force exerted decreases. The relationship is curved, and is described by the following hyperbolic equation:
(P + a) (v + b) = b (Po + a) = constant equation 5-1
where P is force, v is velocity of shortening, Po is isometric force, a and b are constants. This equation can be rearranged to the following (MacIntosh, Herzog, Suter, Wiley, & Sokolosky, 1993):
P = [b (Po + a) ( v + b)-1] – a equation 5-2
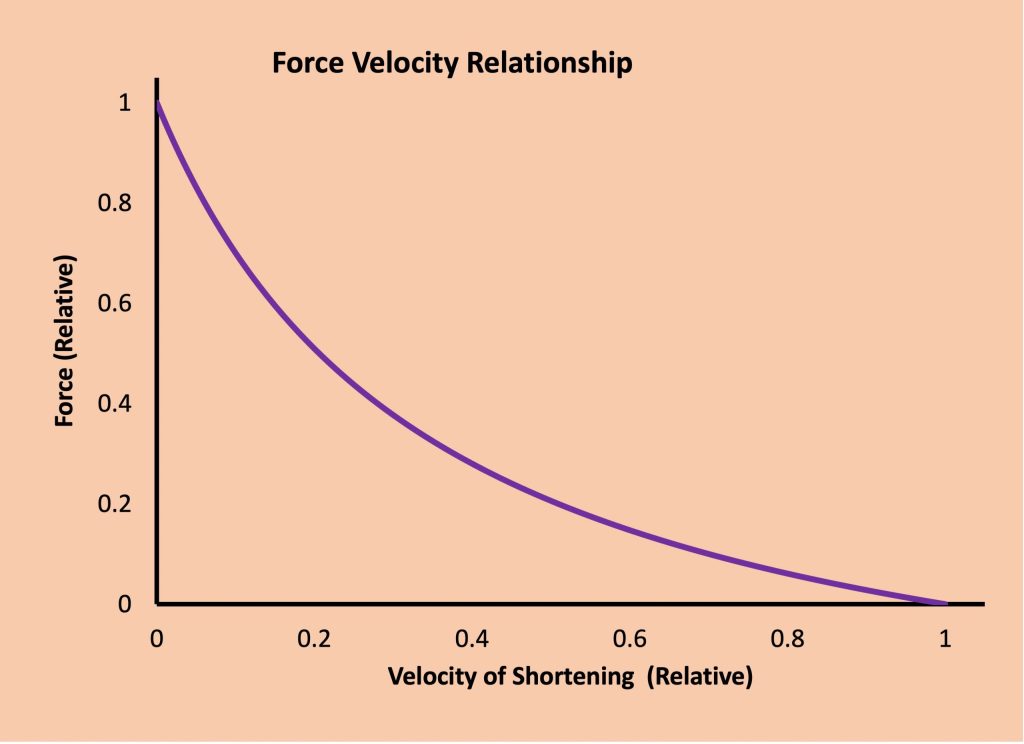
The curvature of the force-velocity relationship is dependent on temperature, fatigue, and fibre-type composition. The ratio of a:Po from the above equation defines the curvature. The smaller the value of this ratio, the greater is the curvature. The curvature is increased as temperature decreases. This is particularly important to understand the extreme curvatures of some published work on skeletal muscle (Hill, 1938). These measures were obtained in amphibian muscle at a temperature ranging from 0 to 25C, and have an a:Po ratio near 0.22. More physiological assessments of human muscle, in vivo, have yielded less curvature (a:Po =0.22 to 0.48) (Wilkie, 1950) to little or no curvature (MacIntosh et al., 1993). Fatigue can apparently have varied effects on the force-velocity relationship, and it is not clear why these differences have been observed. Some reports of the impact of on the force-velocity relationship indicate greater curvature (De Ruiter, Jones, Sargeant, & De Haan, 1999) while other reports show decreased curvature (Andrea N. Devrome & MacIntosh, 2018). Additional work is clearly needed to understand these differences.
One thing is clear, the persistent changes observed in recovery are minimal with respect to the curvature. When mammalian muscle recovers from fatigue, low-frequency fatigue persists but the curvature of the force-frequency relationship returns to the control value (A. N. Devrome & MacIntosh, 2007).
Slow-twitch fibres have greater curvature in their force-velocity relationship than do fast-twitch fibres. This probably relates to the mechanism for the curvature described below. Combining fast and slow-twitch fibres in the same muscle accentuates the curvature. This is evident in figure 5-17 below, which shows 5 theoretical muscles with varying fibre-type composition (30-70% fast-twitch).
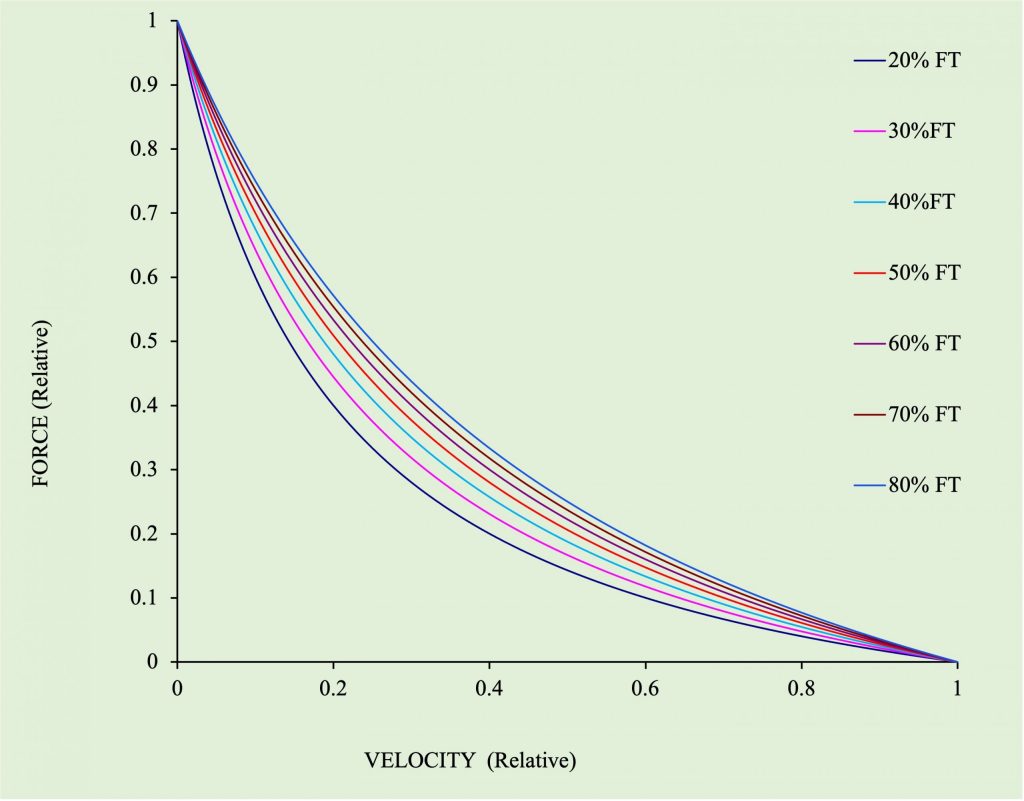
Mechanism of Decreased Force with Increased Velocity of Shortening
Logistically, it can be predicted that there are two factors that contribute to the decrease in force as velocity of shortening increases. These two factors are less force per crossbridge and/or fewer crossbridges. It appears that both of these factors are important in determining the force-velocity relationship. It has been shown that in cardiac muscle, force per crossbridge decreases in a straight line as velocity increases (De Tombe & ter Keurs, 1992). A similar observation was made by Piazzesi and colleagues (2007) for skeletal muscle. However, in this case the linear decline was somewhat delayed (began decreasing after some increase in velocity). If decreased force per crossbridge can account for only a straight linear decrease, then decreased number of crossbridges must account for the remaining decrement in force as velocity increases. This possibility is illustrated in Figure 5-18. The blue line shows the magnitude of difference between the straight linear decrease in force and the curved decrease. This difference is expressed relative to the magnitude of the straight line at that velocity. The value of the blue line at any velocity represents the relative deficit of crossbridges in comparison with the number for an isometric contraction. For example, when velocity is 0.5 of maximal velocity, the deficit is 0.59. This means that only 41% of the number of crossbridges engaged during an isometric contraction will be engaged during this dynamic contraction.
Why are there fewer crossbridges attached as velocity increases? The number of crossbridges bound at one time are dependent on the rate constants for attachment and detachment such that N= f (f + g)-1 (De Tombe & Stienen, 2007). It is generally thought that as shortening velocity increases, g, the rate constant for crossbridge disengagement increases. If this was the only change, then the ratio above would decrease, resulting in fewer crossbridges engaged. However, f, the rate constant for crossbridge engagement may decrease as velocity of shortening increases, contributing further to the crossbridge deficit.
Power–Velocity Relationship
The relationship between and velocity of shortening is dependent on the force-velocity relationship. Power is the product of force and velocity, so this relationship strictly determines the power-velocity relationship. Power of muscle contraction is zero when either force or velocity is zero. This happens at each end of the curve, so power is zero when velocity is zero and when velocity is maximal. The shape of the power-velocity relationship predicts the conditions where power is the highest. The velocity at which power is the highest is called the optimal velocity.
The curvature of the force-velocity relationship dictates the shape of the power-velocity relationship. As a/Po decreases (curvature increase), peak power decreases and optimal velocity decreases. These interactions can be seen in Figure 5-19.
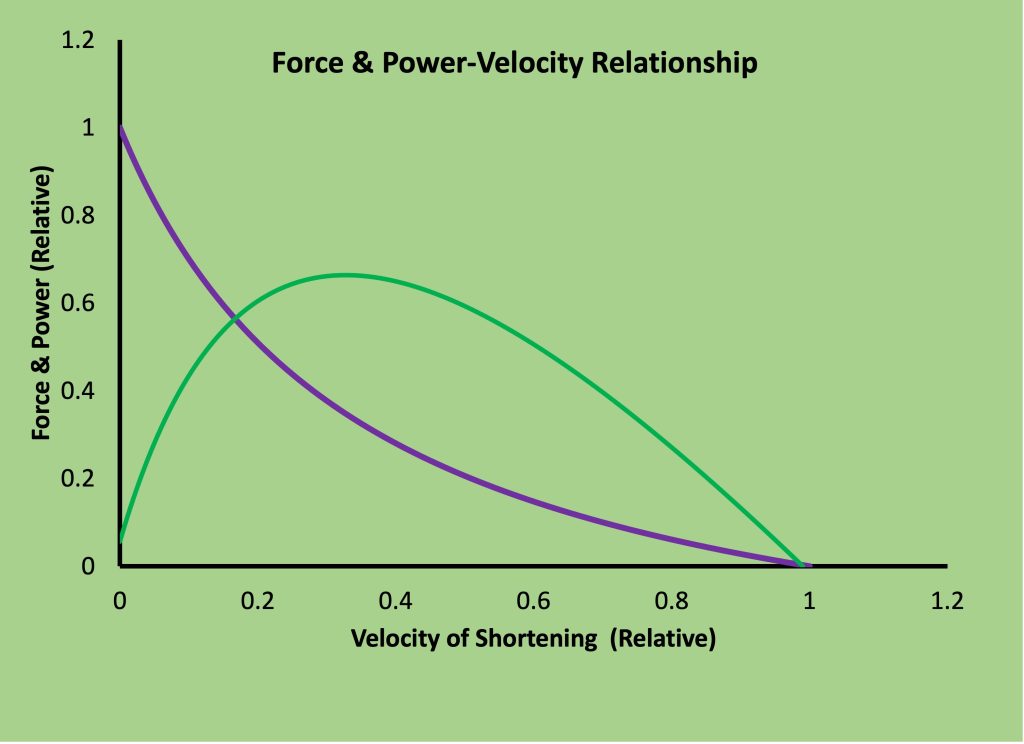
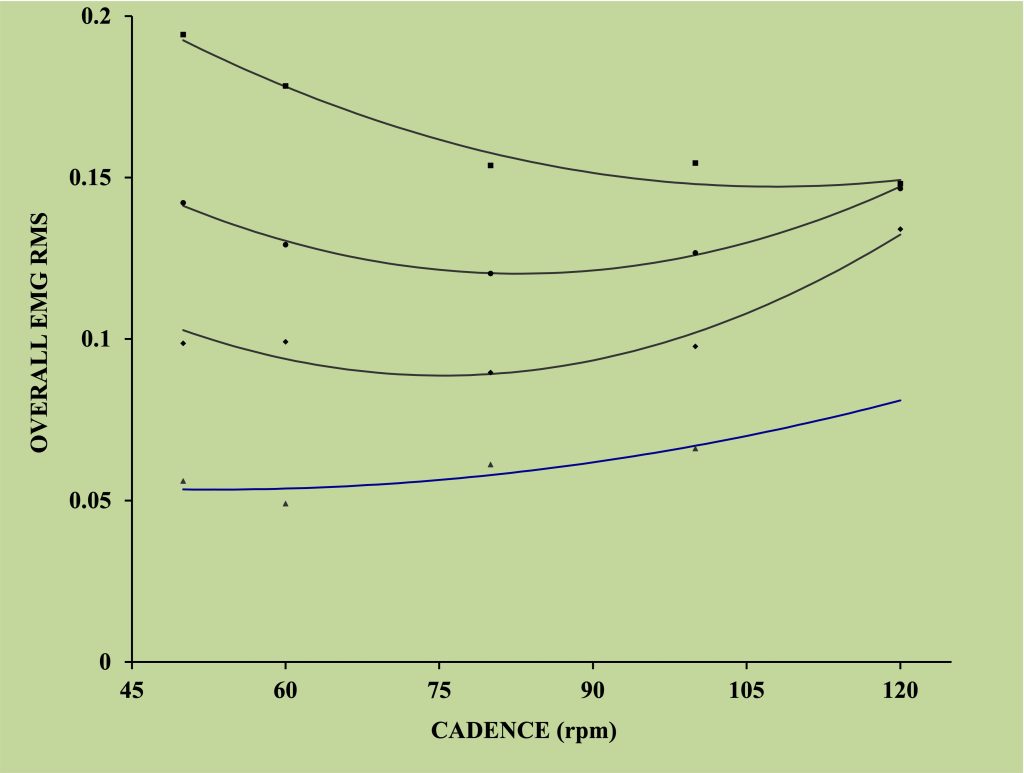
Figure 5.20 EMG-cadence relationship at 4 power outputs for an individual. This figure shows the relationship between magnitude of EMG (quantified as root mean square) for an average of 7 muscles involved in cycling at a variety of cadences at each of 4 power outputs from lowest line to upper line representing 100 W, 200 W, 300 W and 400 W. The data show that muscle activation is minimal at a unique cadence for each power output. The optimal cadence increases as power output increases. These data are from a single subject in the study described in the paper by MacIntosh and colleagues (2000).
Cycling: An Example of Dynamic Muscle Use
Cycling is a common exercise studied by exercise physiologists. Cycle ergometers have been available for research for as long as there have been exercise physiologists and these ergometers allow quantification of power output while keeping the subject stationary for monitoring heart rate, oxygen uptake, and of several muscles.
Muscle Activation In Exercise
It is not easy to quantify motor unit recruitment during cycling exercise. That would require intramuscular needle or fine wire EMG . However, a generalized notion of muscle activation can be obtained from measurement of the magnitude of surface EMG (integrated EMG or root mean square). Muscle activation is increased by increasing the frequency of activation on individual motor units (also known as rate coding), and by recruiting additional motor units. The pattern of muscle activation required depends not only on output but also on the cadence (crank revolutions per minute). At any cadence, muscle activation will increase with increased power output (MacIntosh, Neptune, & Horton, 2000). However, at a given power output, there is a cadence that will require the lowest amount of muscle activation and muscle activation must increase with lower or higher cadence at that power output. Figure 5-22 illustrates this interesting muscle activation requirement, which is dependent on the force-velocity properties of the key muscles involved in cycling.
Research Highlight: Presentation of article by C. Maganaris, 2003
Force-length characteristics of the in vivo human gastrocnemius muscle. Clinical Anatomy 16: 215-223. DOI: 10.1002/ca.10064
Ideally, you should read the paper by Maganaris (2003) before reading the following section of this chapter. The purpose of this paper was to evaluate the structure of the medial and lateral gastrocnemius muscles and Achilles tendon during maximal isometric (fixed-end) contractions initiated at a range of ankle joint angles. In this way, the force-length relationship could be evaluated in vivo. It is acknowledged in the Introduction of this paper that it is difficult to know the architecture of muscle as force develops; tendon stretches and fibres shorten. However, ultrasound imaging can be used to see what is happening during a muscle contraction.
The methods used for this study are fairly standard for current in vivo human muscle measurements. Note that the authors obtained approval from a local ethics committee before proceeding with the study and that their subjects gave informed written consent to participate in the study. The author used several techniques to assure that what was measured is accurate. The general approach is to ask their subjects to exert maximal effort against the dynamometer with the ankle at a variety of angles from -20 (20º of dorsiflexion relative to a foot in the neutral position (foot perpendicular to the shank)) to +30º (30º of plantarflexion relative to a foot in the neutral position). This is equivalent to a range from 70º to 120º for an angle measured between the foot and the shank.
Ankle plantar flexor was measured, correcting for the moment needed to overcome gravitational force (unmeasured force exerted by the ankle plantar flexors to support the weight of the foot and the equipment). Fascicle length and pinnation angle was measured with ultrasound imaging. To calculate muscle force from the measured moment, it is necessary to know the length of the arm. Moment arm length was estimated by the tendon travel (or excursion) method. This method uses ultrasound images of the muscle-tendon junction at two ankle positions, while the muscle is inactive, to allow determination of the change in position of the muscle-tendon junction. The moment arm is estimated as the change in position (measured in mm) relative to the change in angle (measured in radians). It is important that the moment about the ankle not change between these measurement positions, because this would potentially change the length of the tendon and violate the criteria for the tendon travel method. This technique assumes that a joint is like a pulley and that the tendon will move a distance equal to 1 radius as the joint moves through 57º (one radian).
The plantar flexor is generated by a number of muscles, including the medial and lateral gastrocnemius muscles. When the knee is straight (180º), the gastrocnemius generates considerable force. However, when the knee is at an angle less than 90º, the gastrocnemius muscle is thought to be at such a short length that it is incapable of generating force that would be measured as a moment at the ankle. The author took advantage of this property to subtract the moment generated with the knee at 120º of flexion with the ankle at each of the standard positions. This position of the knee would create a knee angle between the thigh and the shank of 60º. By performing this subtraction, the moment generated by all muscles crossing only the ankle joint would be subtracted from the moment generated by all muscles contributing to the ankle moment, including the gastrocnemius muscles. The difference would be the moment generated by the gastrocnemius muscles (medial and lateral head).
Dividing the net (peak moment of the gastrocnemius muscles minus passive moment) by the moment arm yielded the active force exerted on the tendon. Note that the author never presents the passive moment and does not present the initial fascicle length. For this reason, it is difficult to know how much the fascicles shortened during these contractions. Force generated by the fascicles was estimated by considering that force was exerted at some angle relative to the line of action of the muscle. Force exerted on the tendon was calculated by multiplying the measured moment by the cosine of pinnation angle. This is equivalent to dividing the force by the cosine of the pinnation angle (as stated in the paper) to yield moment.
To be certain that the effort of their subjects was maximal, the author used twitch interpolation. A superimposed twitch would reveal negligible force if the person was able to generate a true maximal effort. This technique is further described in Chapter 12.
Based on previous research, it was calculated that the medial head of the gastrocnemius (GM) provided 70% of the gastrocnemius force and the lateral head of the gastrocnemius (GL) provided 30%. This is based on the fact that the cross-sectional area of the medial gastrocnemius is greater than that of the lateral gastrocnemius. It was necessary to separate these synergistic muscles because a graph of fascicle length vs. active force is presented in the results and it is clear that the two muscles operate at a different fascicle length. This graph shows the primary observation of this study. Active force for each of these muscles increases linearly over the entire range of fascicle lengths. This linear change in force can be interpreted to mean the muscles are on the ascending limb of the force-length relationship (see Figure 5-21).
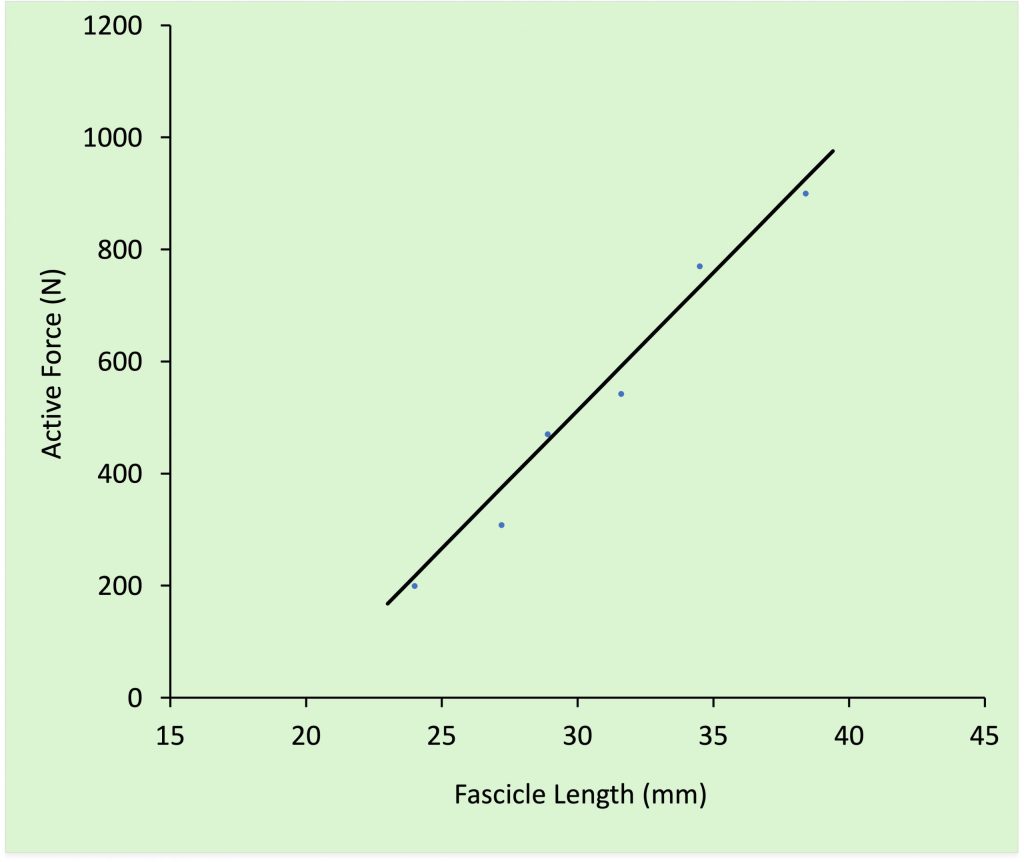
In the discussion of the paper, the author presents an estimate of the sarcomere length of the medial and lateral gastrocnemius muscles over the range of measured active force. It is assumed that the medial gastrocnemius muscle fibres have 17,600 sarcomeres in series and by dividing the measured fascicle length by the number of sarcomeres, the sarcomere length can be estimated. It is estimated that the sarcomeres range from 1.4 to 2.2 µm. This seems like a short sarcomere length for this muscle, considering the filament lengths of human muscle (see Figure 5-23 above). It seems unlikely that any active force could be generated at a sarcomere length below 1.6 µm. Most muscle physiologists would argue that the muscle should be at or near the plateau of the force-length relationship during maximal activation. The author argues that this range of sarcomere lengths is reasonable because the muscles would normally be used in submaximal contractions, and this would result in less stretch of the tendon and therefore a longer sarcomere length. The plateau of the force-length relationship should be 2.6-2.8 µm.
Fukunaga et al (2001) used a similar assumption to estimate that sarcomere length in the medial gastrocnemius muscle during walking was in the range of 2.75-2.92 µm. It would have been nice to know the resting length of the fascicle in this study.
—
Summary
The structure of muscle, presented in Chapter 4 relates well to the function of muscle presented here in Chapter 5. Muscle is organized into motor units, groups of cells that are activated together with a series of action potentials on a given axon. When an action potential arrives at the nerve terminal, neuromuscular transmission allows activation of all of the muscle fibres associated with that motor unit. Excitation-contraction coupling is the process that turns the neural signal into a contraction. The action potential is transmitted along the sarcolemma and into the transverse tubules where the receptors detect the voltage change. The receptors signal the ryanodine receptors to open and allow Ca2+ to flow out of the terminal cisternae into the cytoplasm. Ca2+ initiates the contraction, which can be fixed-end or dynamic (shortening or lengthening The magnitude of response is dependent on many factors, including the concentration of Ca2+ achieved with the activation. Sensitivity to Ca2+ can also be altered. The energy for muscle contraction comes from adenosine triphosphate a universal biological energy source. Fundamental properties of muscle dictate the nature of the contractile response. These properties include the force-length relationship, the force-frequency relationship, the force-velocity relationship and the power-velocity relationship.
Exercises or Topics for Discussion:
- What are the factors that could allow two individuals with the same maximal isometric force when one of them was 2 m in height and the other was 1.6 m in height?
- How would you determine the force-length relationship for the elbow flexor muscles?
- Describe the sequence of events in excitation-contraction coupling.
- What factors would be important in determining how fast a catapult could launch a pumpkin and how does this relate to muscle function?
References
Balnave, C. D., & Allen, D. G. (1995). Intracellular calcium and force in single mouse muscle fibres following repeated contractions with stretch. Journal of Physiology, 488, 25-36.
Binder-Macleod, S. A., Lee, S. C. K., Fritz, A. D., & Kucharski, L. J. (1998). New look at force-frequency relationship of human skeletal muscle: effects of fatigue. Journal of Neurophysiology, 79(4), 1858-1868.
Brown, I. E., & Loeb, G. E. (1999). Measured and modeled properties of mammalian skeletal muscle. I. The effects of post-activation potentiation on the time course and velocity dependencies of force production. Journal of Muscle Research and Cell Motility, 20(5-6), 443-456.
De Ruiter, C. J., Jones, D. A., Sargeant, A. J., & De Haan, A. (1999). The measurement of force/velocity relationships of fresh and fatigued human adductor pollicis muscle. European Journal of Applied Physiology & Occupational Physiology, 80(4), 386-393.
De Tombe, P. P., & Stienen, G. J. (2007). Impact of temperature on cross-bridge cycling kinetics in rat myocardium. J Physiol, 584, 591-600. doi:10.1113/jphysiol.2007.38693
De Tombe, P. P., & ter Keurs, H. E. D. J. (1992). An internal viscous element limits unloaded velocity of sarcomere shortening in rat myocardium. Journal of Physiology, 454, 619-642.
Devrome, A. N., & MacIntosh, B. R. (2007). The biphasic force-velocity relationship in whole rat skeletal muscle in situ. J Appl Physiol, 102(6), 2294-2300.
Devrome, A. N., & MacIntosh, B. R. (2018). Force-velocity relationship during isometric and isotonic fatiguing contractions. Journal of Applied Physiology. doi:10.1152/japplphysiol.01119.2017
Fabiato, A., & Fabiato, F. (1978). Effects of on the myofilaments and the sarcoplasmic reticulum of skinned cells from cardiac and skeletal muscles. Journal of Physiology, 276, 233-255.
Glass, L. D., Cheng, A. J., & MacIntosh, B. R. (2018). Role of Ca2+ in changing active force during intermittent submaximal stimulation in intact, single mouse muscle fibers. Pflügers Archiv – European Journal of Physiology, 470(8), 1243-1254. doi:10.1007/s00424-018-2143-y
Gordon, A. M., Huxley, A. F., & Julian, F. J. (1966). The variation in isometric tension with sarcomere length in vertebrate muscle fibres. Journal of Physiology, 184(1), 170-192.
Gronert, G. A. (1980). Malignant hyperthermia. Anesthesiology, 53, 395-423.
Harrington, W. F., & Rodgers, M. E. (1984). Myosin. Annual Review of Physiology, 53, 35-73.
Hill, A. V. (1928). The Diffusion of Oxygen and Lactic Acid through Tissues. Proceedings of the Royal Society of London. Series B, Biological Sciences, 104(728), 39-96.
Hill, A. V. (1938). The heat of shortening and the dynamic constants of muscle. Proceedings of the Royal Society of London.Series B: Biological Sciences, 126, 136-195.
Huxley, A. F. (1957). Muscle structure and theories of contraction. Progress in Biophysics and Biophysical Chemistry, 7, 255-318.
Huxley, H. E., & Hanson, J. (1954). Changes in the cross-striations of muscle during contraction and stretch and their structural interpretation. Nature, 173(4412), 971-973.
Komi, P. V., & Nicol, C. (2000). Stretch-shortening cycle fatigue. In B. M. Nigg, B. R. MacIntosh, & J. Mester (Eds.), Biomechanics and Biology of Movement (pp. 385-408). Champaign, IL: Human Kinetics. (Reprinted from: IN FILE).
Levine, R. J. C., Kensler, R. W., Yang, Z. H., Stull, J. T., & Sweeney, H. L. (1996). Myosin light chain phosphorylation affects the structure of rabbit skeletal muscle thick filaments. Biophysical Journal, 71, 898-907.
Lieber, R. L., Loren, G. J., & Friden, J. (1994). In vivo measurement of human wrist extensor muscle sarcomere length changes. Journal of Neurophysiology, 71, 874-881.
MacIntosh, B. R. (2003). Role of calcium sensitivity modulation in skeletal muscle performance. News In Physiological Sciences, 18, 222-225.
MacIntosh, B. R. (2017). Recent developments in understanding the length dependence of contractile response of skeletal muscle. Eur J Appl Physiol, 117(6), 1059-1071. doi:10.1007/s00421-017-3591-3
MacIntosh, B. R., Herzog, W., Suter, E., Wiley, J. P., & Sokolosky, J. (1993). Human skeletal muscle fibre types and force:velocity properties. European Journal of Applied Physiology & Occupational Physiology, 67, 499-506.
MacIntosh, B. R., & MacNaughton, M. B. (2005). The length dependence of muscle active force: considerations for parallel elastic properties. Journal of Applied Physiology, 98(5), 1666-1673.
MacIntosh, B. R., Neptune, R. R., & Horton, J. F. (2000). Cadence, power, and muscle activation in cycle ergometry. Medicine and Science in Sports and Exercise, 32(7), 1281-1287.
Maganaris, C. N. (2003). Force-length characteristics of the in vivo human gastrocnemius muscle. Clin.Anat., 16(3), 215-223.
Moore, R. L., & Stull, J. T. (1984). Myosin light chain phosphorylation in fast and slow skeletal muscles in situ. American Journal Physiology – Cell Physiology, 247(5 Pt 1), C462-C471.
Pate, E., Bhimani, M., Franks-Skiba, K., & Cooke, R. (1995). Reduced effect of on skinned rabbit psoas muscle mechanics at high temperatures: implications for fatigue. Journal of Physiology, 486, 689-694.
Persechini, A., Stull, J. T., & Cooke, R. (1985). The effect of myosin phosphorylation on the contractile properties of skinned rabbit skeletal muscle fibers. The Journal of Biological Chemistry, 260(13), 7951-7954.
Piazzesi, G., Reconditi, M., Linari, M., Lucii, L., Bianco, P., Brunello, E., . . . Lombardi, V. (2007). Skeletal muscle performance determined by modulation of number of myosin motors rather than motor force or stroke size. Cell, 131(4), 784-795. doi:10.1016/j.cell.2007.09.045
Podlubnaya, Z., Kakol, I., Moczarska, A., Stepkowski, D., & Udaltsov, S. (1999). Calcium-induced structural changes in synthetic myosin filaments of vertebrate striated muscles. Journal of Structural Biology, 127(1), 1-15.
Pollack, G. H. (1983). The cross-bridge theory. Physiological Reviews, 63, 1049-1113.
Rassier, D. E., & MacIntosh, B. R. (2002). Sarcomere length-dependence of activity-dependent twitch potentiation in mouse skeletal muscle. BMC Physiology, 2(19), 1-8.
Rassier, D. E., MacIntosh, B. R., & Herzog, W. (1999). Length dependence of active force production in skeletal muscle. Journal of Applied Physiology, 86(5), 1445-1457.
Sale, D. G. (2002). Postactivation potentiation: role in human performance. Exercise and Sport Sciences Reviews, 30(3), 138-143.
Stephenson, E. W. (1981). Activation of fast skeletal muscle: contributions of studies on skinned fibers. American Journal Physiology – Cell Physiology, 240(1), C1-C19.
Tihanyi, J., Apor, P., & Fekete, G. (1982). Force-velocity- characteristics and fiber composition in human knee extensor muscles. European Journal of Applied Physiology & Occupational Physiology, 48(3), 331-343. doi:10.1007/BF00430223
Wang, Y. P., & Fuchs, F. (2000). Length-dependent effects of osmotic compression on skinned rabbit psoas muscle fibers. Journal of Muscle Research and Cell Motility, 21(4), 313-319.
Wendt, I. R., & Stephenson, D. G. (1983). Effects of caffeine on Ca-activated force production in skinned cardiac and skeletal muscle fibres of the rat. PflÅgers Archiv: European Journal of Physiology, 398(3), 210-216. doi:10.1007/BF00657153
Wilkie, D. R. (1950). The relation between force and velocity in human muscle. Journal of Physiology, 110, 249-280.

