Repeated dosing calculations
The aim of repeated dosing is to achieve an average steady state plasma concentration (Css) that lies within the therapeutic window – preferably towards the lower end of that window. For many drugs, the window is extremely wide and a calculation needs only to consider the dosing rate that will yield the required average concentration. Generally, these calculations have been done for you – they are what have led to the recommended dosing regimen in your drug formulary or on the drug’s data sheet. As a result of differences in patient physiology (particularly with regard to differences in intrinsic clearance for a drug between different patients), a fixed dosing regimen will result in different steady state concentrations for a drug in different patients. However, the therapeutic window for most drugs is sufficiently wide that the steady state concentration still lies well within the limits of the window, and it is not necessary to adjust the dose. For those drugs that have a narrow therapeutic index and for which there is a significant risk associated with plasma drug concentrations falling outside the window, drug formularies will usually provide recommendations on dosing changes that need to be considered when a patient has a disease affecting drug pharmacokinetics, such as chronic kidney disease.
For drugs with a narrow therapeutic window, consideration may also need to be given to the variation between peak and trough (Cmax and Cmin) concentrations, so that the chosen combination of dosing interval and dose size that gives the required dosing rate does not result in peak and trough concentrations that extend beyond the upper and lower limits of the therapeutic window. The ratio of peak to trough concentrations depends only upon the dosing interval and the half life for elimination. The actual concentrations are irrelevant with respect to calculation of this ratio. If a drug is administered IV once every half life then at steady state, concentration of drug in the plasma drops by 50% from peak to trough. This is because, at steady state, the rate of drug entering the body is identical to the rate of drug leaving the body, and as such, the Cmax:Cmin ratio would be 2. If a drug is administered twice every half life then the Cmax:Cmin ratio would be 1.414. It is irrelevant what the average plasma concentrations actually are.
For a drug that is eliminated with first order kinetics, the average drug concentration in the plasma can be calculated by dividing the AUC by the dosing interval, τ, where AUC refers either to the AUC from t=0 to t=∞ following a single IV dose, or to the AUC between two consecutive doses at steady state. The entry for area under the curve provides further explanation of this point. The midpoint between Cmax and Cmin for repeated IV administrations at steady state approaches the (fixed) value of the average steady state concentration as the interval between doses, τ, tends towards zero. However, as the dosing interval is increased (while maintaining the same dosing rate and thus maintaining an identical Css), the Cmax:Cmin ratio increases while the midpoint between Cmax and Cmin also moves increasingly above the average Css. For example, when τ is equal to the elimination half-life, the average concentration lies at a point around 56% of the distance from Cmax to Cmin, while this increases to around 61% when τ is twice the elimination half-life, 65% when τ is three times the elimination half-life and 69% when τ is four times the elimination half-life. This explains why a target concentration is generally chosen which is a little below the midpoint between Cmax and Cmin; this is demonstrated in the calculation example, below.
Example calculation
An antibiotic has a volume of distribution of 350 litres and an elimination half-life of 4.6 hours. Oral bioavailability is 20%. Plasma concentrations above 25 µg/litre may cause irreversible hearing damage, while a minimum bactericidal concentration of at least 15 µg/litre must be maintained at all times. Design an appropriate oral dosing regimen for this antibiotic drug.
First, decide upon a suitable average steady state plasma concentration. The therapeutic window lies between 15 and 25 µg/litre, and a suitable choice for steady state concentration generally lies a little below the median value in the the therapeutic window, which is 20 µg/litre. In this example, a choice of 19 µg/litre would therefore be appropriate. At this concentration, 60% of the difference between Cmax (25 µg/litre) and Cmin (15 µg/litre) lies above the chosen average Css, and 40% below the chosen value.
The dosing rate required to achieve this concentration in the plasma should then be determined. This can be calculated from the equation below:
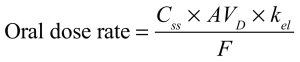
From the elimination half-life of 4.6 hours can be calculated a value for kel of 0.15/h (from 0.693/4.6h). Then this value, plus those provided, can be inserted into the above equation:
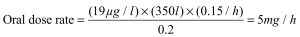
We have now calculated that a dose rate of 5 mg/hour will achieve a steady state concentration in the plasma of 19 µg/litre. We must now determine the combination of dose size and interval that will achieve this dosing rate while ensuring that peak and trough concentrations remain within the limits of the therapeutic window. The equation to be used is designed for IV administration; the current example is an oral dosing scenario, in which peaks and troughs will be less extreme than with IV dosing. As such, calculation of a Cmax:Cmin ratio suitable for IV dosing will provide a value that will certainly ensure drug concentrations remain well within the therapeutic window limits when oral administration is used.
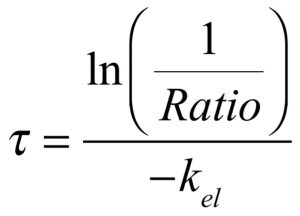
The equation in the upper panel (left) allows calculation of the dosing interval that will achieve a Cmax:Cmin ratio equal to the value inserted into the equation. The maximum ratio permissible for the antibiotic is 25 µg/litre ÷ 15 µg/litre, or 1.67. Inserting this ratio, as well as the elimination rate constant for the antibiotic, into the equation yields the result shown in the lower panel.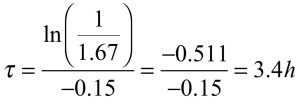
The calculated value for τ of 3.4 hours is the maximum allowable time between consecutive doses, since an interval longer than 3.4 hours would yield a Cmax:Cmin ratio greater than 1.67, and peaks and/or troughs exceeding the limits of the therapeutic window. A shorter dosing interval is permissible, since the ratio would become smaller as both Cmax and Cmin would move closer to the chosen average steady state concentration. In this example, a dosing interval of 3 hours would be suitable.
The required dosing rate to reach the target Css of 19 µg/litre was calculated as 5 mg/hour. If a dosing interval of 3 hours is acceptable, then 15 mg of the antibiotic would be administered orally every 3 hours.
When a patient has a condition affecting drug clearance, such as chronic kidney disease or hepatic insufficiency, the reduced clearance typically results in an increase in the drug’s half life of elimination (and a decrease in kel). When a reduction in dosing rate is necessary in such a patient, this can be achieved by administering the same size of dose at longer dosing intervals. A glance at the equation in the example box above for calculating τ provides an explanation; the maximum allowable value for the dosing interval, τ, is increased as a result of the decrease in kel.
