First-order elimination rate constant

An exponential curve showing first order (concentration-dependent) loss of drug from the plasma is described by an equation for exponential decay (right).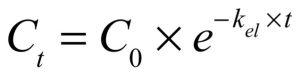 This equation shows that the concentration of drug in the plasma at any time point (t) after IV administration can be found if you know the (theoretical) concentration at time zero (C₀, synonymous with C_p0, which is found by back-extrapolating the curve to the Y-axis, or back-extrapolating the straight line when a logarithmic Y-axis is used) as well as the elimination rate constant, k_el. The elimination rate constant (which has units of “per time”) is a proportionality constant; it tells you what proportion of the remaining drug would be removed over the following minute, or hour (or whatever the unit of time being used is) if the rate of elimination present at that time was maintained for the duration of the subsequent minute, or hour. Similarly, it also tells you what proportion of the volume of distribution would be cleared of drug over the subsequent minute or hour if the rate of elimination that exists at the beginning of that minute or hour was maintained for the entire minute or hour.

For example, if you have 500 mg of drug in the body distributed throughout a volume of distribution of 100 litres, and if the k_el is 0.2 per hour, then the rate of elimination that exists at the beginning of that hour is 0.2 x 500 mg = 100 mg/hour, and so you would lose 100 mg of drug over that hour if the rate of elimination was maintained at 100 mg/hour. Similarly, the proportion of the volume of distribution that would be cleared of drug over that hour would also be 0.2, and so clearance would be 0.2 x 100 litres = 20 litres/hour. HOWEVER, because elimination is a first-order (concentration-dependent) process, then as drug is removed, the rate of elimination falls with time. So as time passes, the rate of elimination will become progressively lower after each minute compared with the starting rate of elimination of 100 mg/hour.

Click here to watch a short vodcast demonstrating what the first-order elimination constant tells you.

This may be most easily understood by putting numbers into the above equation. If our starting concentration in this example is 500 mg in 100 litres, or 5 mg/litre, and k_el is 0.2/hour, what would the concentration of drug be, and what would the new rate of elimination be, after 15 minutes (or 0.25 hours)? 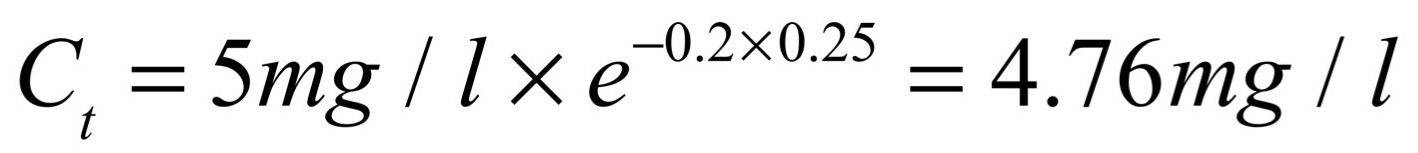As can be seen (left), the concentration would have dropped to 4.76 mg/litre, for a total body content of drug of 476 mg in 100 litres, and so the rate of elimination after 15 minutes would be 0.2 x 476 mg = 95.2 mg/hour (down from 100 mg/hour at time zero). BUT (and here is the critical point about first order rate constants) – if THAT new rate of elimination was maintained for the next hour then 0.2 or 20% of that 476 mg would still be eliminated over the next hour, and 0.2 of the volume of distribution would also still be cleared of drug over the next hour. So the k_el is a constant and it always holds true. The PROPORTION of drug that would be eliminated in unit time is a constant, but the AMOUNT of drug that would be eliminated in unit time becomes progressively smaller as the concentration drops.