Hill-Langmuir equation

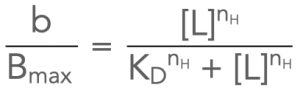This is an equation for a hyperbola that allows you to determine the proportion of total receptors (or other proteins) bound at any given concentration of a ligand, [L], if you know the KD for the ligand interacting with those receptors. In order for binding to show hyperbolic behaviour, the KD for the interaction between ligand and receptor is typically much higher than the concentration of receptors present. Since a therapeutic effect is typically only evident when drug is interacting with a reasonable proportion of the total receptor population, the result of this is that concentrations of drug present are almost always far higher than the concentrations of receptor targets present, and so when a small amount of the free drug binds to the receptors, there is no appreciable change in the concentration of free (unbound) drug.

The equation shown contains an exponential term, nH. This is the Hill coefficient, and for most drugs, it can be assumed to equal 1 and can thus be ignored. For a few ligands that bind to dimeric or multimeric proteins with multiple subunits and multiple ligand binding sites, binding of one ligand to the protein complex may impact binding of further ligands to further binding sites within the same protein complex, either enhancing or attenuating binding. This phenomenon, called cooperativity of binding, is also seen physiologically, for example in the binding of oxygen to haemoglobin. Cooperativity yields binding curves and dose-response curves that are not simple hyperbolas. The figures below show binding curves on linear (left) and logarithmic (right) axes for three ligands that share a common KD value, but with differing Hill coefficients.

(Left panel) Binding curves for three ligands, each with a KD of 10 µM for its target protein. The green dashed line shows binding of a drug ligand with a Hill coefficient of 1. The blue line shows binding of a ligand with a Hill coefficient of 0.4. This drug shows negative cooperativity of binding, meaning that binding of the first ligand reduces the binding affinity of the remaining site(s) for binding of a second ligand. The red line shows binding of a ligand with a Hill coefficient of 3. This drug shows positive cooperativity of binding, meaning that binding of the first ligand increases the binding affinity of the remaining site(s) for binding of a second ligand. (Right panel) The same data are shown plotted on a logarithmic concentration axis, revealing a series of sigmoidal plots of differing steepness. Binding of oxygen to haemoglobin shows positive cooperativity of binding. The physiological consequence of this is that hemoglobin can progress from having no bound oxygen to having four molecules of oxygen bound (corresponding to Bmax) as a result of a relatively small increase in dissolved oxygen concentrations in the pulmonary vasculature, and can then give up all four oxygen molecules as blood passes through tissues in which dissolved oxygen concentrations are a little lower. Without cooperative binding, the modest differences in oxygen concentrations between pulmonary blood and blood elsewhere in the body would have almost no effect on the degree of binding of oxygen to haemoglobin, as the concentration change in oxygen required would span almost two orders of magnitude.

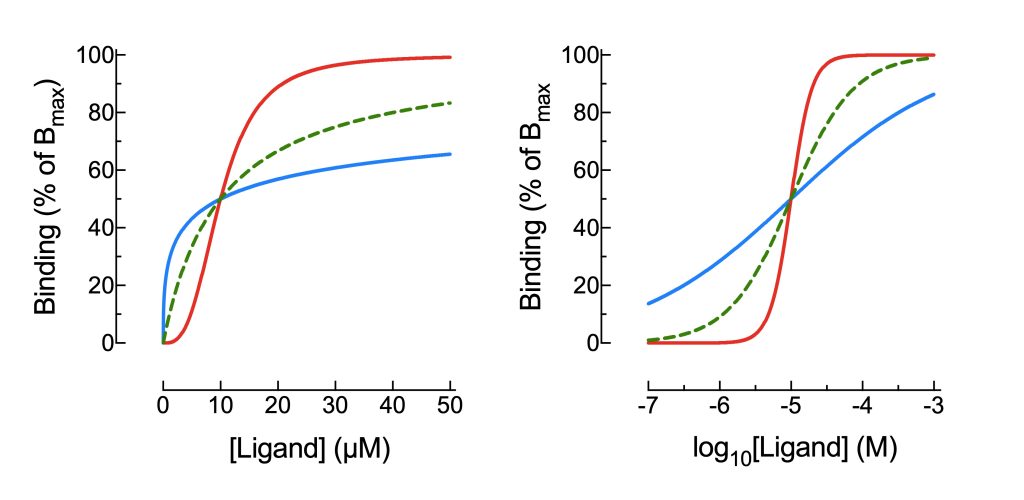
From a clinical therapeutic perspective, the target range for the steady state concentration of a cooperative drug may be narrower, or wider, than for most drugs, but this would be reflected in the recommended dosing regimens, and cooperativity is not an issue you need to be concerned with in relation to clinical use of drugs.

In those situations where a ligand has extremely high affinity for a receptor (such that the KD is down in the same range as the concentration of receptors) OR when the concentration of protein “targets” is extremely high (such as with drug binding to plasma proteins) then depletion of free ligand becomes significant (this is why plasma protein binding has such a significant impact on drug behaviour), and binding is described by a quadratic equation. It is not necessary to be familiar with this equation, but you should be aware that drugs with extremely high affinities for their targets do not follow the same mathematical patterns of pharmacodynamic behaviour seen with most drugs.

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

An ABC of PK/PD Copyright © 2023 by Dr. Andrew Holt is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book