Area under the curve

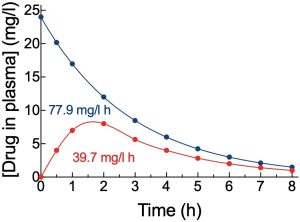
This usually refers to the area under the curve (AUC) for a graph of plasma concentration versus time. The units of AUC are the Y-axis units (units of concentration) multiplied by the X-axis units (units of time); for example, (mg/l)h or (µg/ml)min. There are several ways to calculate AUC, including through use of software, or manually by applying the trapezoidal rule or by a cut-and-weigh technique.

It may be necessary to determine a drug’s AUC in order to calculate oral bioavailability (discussed below), or to determine the non-compartmental apparent volume of distribution (AV_{D area}).

In a single individual, the AUC is proportional to the proportion of the dose of drug that is absorbed into the systemic circulation, and the actual value is impacted by the amount of the drug that is absorbed, and by how rapidly it is then removed. As such, a comparison of an IV dose with a PO dose of the same drug in the same individual on two different occasions will provide two AUC values that allow determination of oral bioavailability (from AUC_PO/AUC_IV). This is because the drug is removed with similar clearance values regardless of the route by which it is administered and the only significant difference between areas under the two curves would be caused by differences in the amount of drug absorbed into the circulation. In the same way, AUC for the same dose of the same drug by the same route in an individual may change if ADME parameters change for the drug in that individual – e.g. altered bioavailability due to a change in Cl_int for a high extraction ratio drug, altered clearance due to a change in Cl_int for a low extraction ratio drug, etc. In the latter example of altered clearance, note that AUC values for PO and IV administration routes in that individual would both change to a similar degree and so bioavailability would not be substantially affected (see example calculation box).

In an intravenous repeated dosing regimen that has reached a steady state concentration, the average concentration in the plasma can be calculated from the AUC between two consecutive doses, divided by the time interval between doses. This average concentration typically lies slightly closer to the trough concentration than to the peak concentration, with this tendency becoming more marked as the time interval between doses becomes larger.

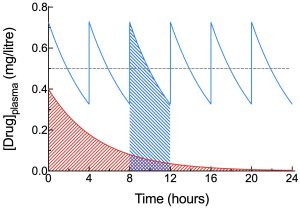
At steady state, it stands to reason that the amount of drug lost from the body between consecutive doses is identical to the amount of drug administered in each dose. As such, the AUC between two consecutive doses at steady state should be similar to the AUC from t=0 to t=∞ (AUC_0-∞) after a single IV dose of the drug (because one full dose of the drug is also lost from the body in such a scenario), assuming the size of the dose is the same in both cases, and assuming there has been no change in drug clearance (as a result of a change in intrinsic clearance, for example) during chronic drug dosing required to reach steady state. This is illustrated in the figure on the right, where the areas highlighted in red and blue hatching are identical in size. Under the entry for clearance, it is shown that total body clearance, Cl_T, may be calculated from Cl_T = Dose/AUC_0-∞. Based on the discussion above, it should be apparent that it is also possible to calculate total body clearance if the AUC between two consecutive doses of drug is known, since this value should be similar to AUC_0-∞. The equation then becomes Cl_T = Dose/AUC_0-τ, where t=0 represents the time at which the first of two consecutive doses is given, and t=τ represents a later time at which the subsequent dose is administered, with the dosing interval being equal to τ.