Affinity
The affinity of a ligand for its target refers to how tightly the ligand binds to the target. The numerical value for affinity, the KD, is the concentration of ligand at which 50% of the targets are bound by ligand in the absence of any other competing ligand(s). The KD may be identified from a hyperbola showing binding plotted against ligand concentration. The lower the KD value, the more tightly the ligand binds.
Collisions between a ligand and a target protein are random. After a collision occurs, a ligand will remain bound for a period of time before it dissociates from the target protein. All other things being equal, a ligand with a higher affinity (lower KD) can be used at a lower dose than a ligand that binds less tightly to the target protein. This reduces the likelihood of off-target side-effects of the drug.
Receptor systems governing processes that are rapid in onset and that require modulation on a very short timescale (for example, activation of neuronal receptors by endogenous neurotransmitters) typically bind endogenous agonists with relatively low affinity. The very brief duration for which the agonist remains bound to the receptor ensures that the cellular response increases and decreases almost in parallel with the (tightly-controlled) concentrations of the endogenous agonist present. For example, synaptic release of acetylcholine at an autonomic ganglion, followed immediately by almost instantaneous inactivation of the transmitter by acetylcholinesterase, is accompanied by a brief influx of cations through receptors that remain activated for barely a millisecond before the transmitter dissociates and is hydrolysed. Though a higher binding affinity would allow much lower concentrations of agonist to be released and then hydrolysed by the system, acetylcholine would remain bound and ion channels would remain open for much longer periods, uncoupling ion flux from synaptic concentrations of transmitter. Instead, efficiency of use for low affinity agonists can be achieved through the redundancy of spare receptors.
The following details provide a more in-depth explanation of the meaning of KD and the importance of association and dissociation rates, for students who wish to know more.
Mathematically, the KD is an equilibrium constant, specifically a dissociation constant, for equilibrium binding between a ligand, L, and a protein, P:

As indicated, the KD is equal to ([L][P])/[LP] at equilibrium (equation (i) in the example below), and also to the value obtained by dividing koff, the rate constant for ligand dissociation (units of s-1), by kon, the rate constant for ligand association (units of M-1s-1) (equation (ii) in the example below).
As an example, consider the scenario where a ligand is applied at a concentration of 15 nM to a population of target proteins at a concentration of 10 pM. The ligand is present in large (1500-fold) excess over the target proteins – this is the case for most ligands at concentration that bind to an appreciable portion of their targets – with the result that when some of the ligand binds to a portion of the target proteins, there is no appreciable change in the concentration of unbound ligand. However, there is a clear increase (from an initial value of 0) in the proportion of target proteins bound by a ligand. In this example, 30% (3 pM) of the target proteins are bound at a ligand concentration of 15 nM, leaving 7 nM unoccupied.
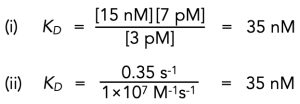
It should be apparent from equation (i), above, that as the concentration of ligand, [L], increases, the concentration of unoccupied protein, [P] in the numerator, will decrease while the concentration of the ligand-protein complex, [LP] in the denominator, will increase. When [L] reaches the KD value of 35 nM, values for [P] and [LP] will be identical, at 5 pM – in other words, 50% of the target proteins are bound by ligand.
In equation (ii), above, a value for kon (the denominator of the equation) has been chosen that is, by convention, fairly typical of rate constants for association of a small ligand with a large protein target. The value of this second-order rate constant itself indicates the number of complete, distinct association events that could occur in one second between a single protein target and a ligand present at a concentration of 1 M. As such, a value for kon of 1×107 M-1s-1 suggests that a single association event takes 1/1×107 s, or 0.1 µs, to occur. More intuitively, multiplying the rate constant (1×107 M-1s-1 ) by [L] and [P], if both L and P were present at a concentration of 1 M, yields a value for the initial (and extremely short-lived) rate of formation of the LP complex of 107 Ms-1. With the more physiologically relevant values from the example above, with [L] = 15 nM and [P] = 10 pM, the concentration of [LP] would increase at an initial rate of (1×107 M-1s-1 × 15 nM × 10 pM), or 1.5 pM s-1. At equilibrium, this association rate would have slowed somewhat due to the reduction in the concentration of free P, to (1×107 M-1s-1 × 15 nM × 7 pM), or 1.05 pM s-1.
Rate constants for associations between ligands and target proteins have historically been considered to lie within an order of magnitude of around 1×107 M-1s-1, between 1×106 M-1s-1 for slower events, to 1×108 M-1s-1 where the rate of association is limited largely by the rate at which a ligand can diffuse through an aqueous environment towards its binding site on a target protein. As such, binding affinities were thought to correlate more closely with values for koff. More recently, it has become clear that values for association rate constants for many drugs lie across a wider range, between 1×104 M-1s-1 and 1×108 M-1s-1, and it is now recognised that variations in kon are just as important as those in koff with respect to the impact upon drug binding affinities and binding behaviour.
The information provided by the first-order rate constant for dissociation of the LP complex, koff, is very similar to that provided by other first-order pharmacokinetic rate constants such as kel. This value indicates the proportion of the LP complex that breaks apart in unit time to yield free L and unoccupied P, and the rate at which dissociation occurs is found by multiplying the dissociation rate constant by the concentration of the LP complex. In the example above, this rate would be maximal once equilibrium is reached, and would equal 3 pM × 0.35 s-1, or 1.05 pM s-1. You will note that this value is identical to the association rate at equilibrium, calculated above. At equilibrium, of course, by definition the (forward) rate of association is equal to the (reverse) rate of dissociation.
There is also a half-life that can be obtained for the dissociation process, from 0.693/ koff; in the example above, the dissociation half-life would be equal to 0.693/0.35 s-1, or 2 seconds. This value tells us that if we were to place a population of LP complexes into a large volume of aqueous buffer, the complex would dissociate with a half life of 2 seconds, and almost all of the protein would exist as free P within 5 half-lives, or 10 seconds.
Another useful value that can be obtained directly from koff is the target residence time for the drug. This value, which is equal to 1/koff, is the average time for which a drug remains bound to its target protein before dissociating (in other words, individual drug molecules may remain bound to a target for much shorter, or much longer, periods, either side of the average residence time). In the above example, the target residence time would be 2.86 seconds. Drugs that have very low koff values have correspondingly long residence times, and are often referred to as “slow-off” drugs.
Although slow-off compounds do not bind irreversibly to their targets, they share many of the behavioural attributes of irreversible drugs. For example, drugs with long residence times may remain bound to their targets long after tissue concentrations of free drug have been depleted through clearance, thereby uncoupling the duration of effect from pharmacokinetic control of drug concentrations in tissues. Slow-off drugs can be particularly effective in circumstances where there is likely to be significant competition for binding, such as when the drug targets a synaptic receptor for a neurotransmitter, quantal release of which results in high synaptic concentrations of the endogenous agonist. In such a situation, a slow-off drug could remain bound, while a drug with a higher koff would be more likely to dissociate and might have very little opportunity to rebind in the face of overwhelming levels of competing neurotransmitter.
There may also be an added benefit of reduced severity of off-target side effects. Even if the KD values for the slow-off drug are similar for its primary target and for a secondary protein through which off-target side-effects are induced, a much longer target residence time for the primary target results in a prolonged therapeutic effect that is accompanied only initially by a much shorter period during which off-target side-effects are experienced before unbound drug redistributes from the tissues back to the plasma, leaving occupied primary targets and unoccupied secondary proteins.
The rate constant for association clearly contributes to the drug’s binding affinity, with higher kon values resulting in lower KD values and higher binding affinity. Drugs with very high kon values are referred to as “fast-on” drugs, and it is not surprising that the drugs with highest binding affinities and longest target residence times are “fast-on, slow-off” compounds. In contrast, “slow-on, fast-off” ligands have low binding affinity, very short target residence times and are not generally suited for use as therapeutic agents.
Although target residence time is equal to 1/koff and is independent of kon, fast-on drugs may experience extended durations of effect as a result of a phenomenon termed drug rebinding. When the rate constant for association is as large as, or larger than, the rate constant for diffusion of free drug away from the target, drug that dissociates from a target is more likely to re-associate with the same target, or with another target in close proximity, than to diffuse away into the cytosol or extracellular fluid. When target proteins are present on a cell surface, dissociation of drug from those proteins into the aqueous environment in immediate proximity to the membrane can elevate the localised concentration of drug to a value significantly higher than the concentration of free drug in solution further from the membrane. Since association rate is equal to kon × [L] × [P], this increase in [L] serves to increase the likelihood of rebinding of the drug, and in tissues with high concentrations of receptor, the increase in [P] and the consequently greater impact on elevating localised drug concentrations further increase rebinding.
The table below illustrates a variety of combinations of values for kon and koff that generate four groups of drugs, with the members of each group sharing a common KD for binding affinity. Barely a decade ago, drugs with similar binding affinities for a common target would have been considered as sharing similar binding properties, and as likely to evoke similar therapeutic effects with respect to responses dependent upon binding behaviour. However, in addition to KD, target residence time and rebinding potential should also be considered. Consider the example of a receptor for which the signal transduction pathway that links agonist binding to a cellular response is a slow process. Perhaps it is more important for an agonist to remain bound to the receptor for a prolonged period in order to generate an intracellular signal sufficiently large to elicit a cellular response, than for the agonist simply to bind with high affinity. Simply put, one lower affinity binding event with a target residence time of 30 seconds may be able to generate a cellular response that six higher-affinity binding events with an average target residence time of 5 seconds each, can not.
In the table, rebinding potential is indicated as being greater for fast-on ligands of lower binding affinity, based on the assumption that lower affinity drugs are, through necessity, probably present at higher concentrations, and the association rate depends upon ligand (and target) concentrations in addition to the value of kon.
| kon (M-1s-1) | On label | koff (s-1) | t½ off |
Off label | KD | Target residence time | Rebinding potential |
| 3×107 | Fast on | 3×10-5 | 6.4 h | Slow off | 1 pM | 9.26 h | + |
| 1×106 | 1×10-6 | 8 days | Slow off | 1 pM | 11.6 days | ||
| 5×104 | Slow on | 5×10-8 | 5.3 months | Slow off | 1 pM | 7.7 months | |
| 3×107 | Fast on | 0.003 | 3.9 min | 100 pM | 5.6 min | ++ | |
| 1×106 | 0.0001 | 1.9 h | Slow off | 100 pM | 2.8 h | ||
| 5×104 | Slow on | 5×10-6 | 1.6 days | Slow off | 100 pM | 2.3 days | |
| 3×107 | Fast on | 0.3 | 2.3 s | Fast off | 10 nM | 3.3 s | +++ |
| 1×106 | 0.01 | 69 s | 10 nM | 100 s | + | ||
| 5×104 | Slow on | 0.0005 | 23 min | Slow off | 10 nM | 33 min | |
| 3×107 | Fast on | 30 | 0.02 s | Fast off | 1 µM | 0.03 s | ++++ |
| 1×106 | 1 | 0.7 s | Fast off | 1 µM | 1 s | ++ | |
| 5×104 | Slow on | 0.05 | 13.9 s | 1 µM | 20 s |
For reasons such as those described above, the pharmaceutical industry no longer focuses solely on identifying ligands with high binding affinity; they also now consider target residence time and the potential for slow-off ligands for those receptors where residence time has a major impact upon the drug’s effectiveness, and also association rate constants where rebinding of fast-on ligands may offer advantages, or present obstacles, compared with drugs that associate at more modest rates.

